【题目】计算:
(1)16÷(﹣![]() )﹣3﹣(﹣
)﹣3﹣(﹣![]() )×(﹣4)
)×(﹣4)
(2)2(a2b+ab2)﹣2(a2b﹣1)﹣ab2+2
(3)(a﹣b﹣2)(a﹣b+2)
(4)899×901+1
参考答案:
【答案】(1)﹣2![]() ;(2)ab2+4;(3)a2﹣2ab+b2﹣4;(4)810000.
;(2)ab2+4;(3)a2﹣2ab+b2﹣4;(4)810000.
【解析】
按照有理数混合运算的顺序,先乘方,再乘除后加减,有括号的先算括号里面的,计算过程中注意正负符号的变化.
原式去括号合并即可解得最简值.
先将原式变形为[a+(b-2)][a-(b-2)],然后再利用平方差公式和完全平方公式进行计算即可.
899可以写成900-1而901写成900+1,899×901就是(900-1)(900+1)就可以利用平方差公式,比较简单的计算出式子的值.
(1)原式=16÷(﹣8)﹣![]() ×4=﹣2﹣
×4=﹣2﹣![]() =﹣2
=﹣2![]() ;
;
(2)原式=2a2b+2ab2﹣2a2b+2﹣ab2+2=ab2+4;
(3)原式=(a﹣b)2﹣4=a2﹣2ab+b2﹣4;
(4)原式=(900﹣1)×(900+1)+1=9002﹣1+1=810000.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乒乓球的质量检验结果如下:
抽取的乒乓球数n
50
100
200
500
1000
1500
2000
优等品的频数m
48
95
188
x
948
1426
1898
优等品的频率
 (精确到0.001)
(精确到0.001)0.960
y
0.940
0.944
z
0.951
0.949
(1)根据表中信息可得:x=______,y=______,z=______;
(2)从这批乒乓球中,任意抽取一只乒乓球是优等品的概率的估计值是多少?(精确到0.01).
-
科目: 来源: 题型:
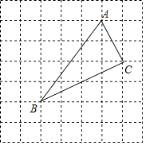
查看答案和解析>>【题目】如图,在7×7网格中,每个小正方形的边长都为1.
(1)建立适当的平面直角坐标系后,若点A(1,3)、C(2,1),则点B的坐标为______;
(2)△ABC的面积为______;
(3)判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组在“用频率估计概率”的实验中,统计了某种频率结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( )

A. 掷一枚质地均匀的硬币,落地时结果是“正面向上”
B. 掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6
C. 在“石头剪刀、和”的游戏中,小明随机出的是“剪刀”
D. 袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球
-
科目: 来源: 题型:
查看答案和解析>>【题目】线段AB=12cm,点C在线段AB上,点D、E分别是AC和BC的中点.
(1)若点C恰好是AB中点,求DE的长.
(2)若AC=4cm,求DE的长.
(3)若点C为线段AB上的一个动点(点C不与A,B重合),求DE的长.
-
科目: 来源: 题型:
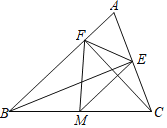
查看答案和解析>>【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,BC=10.
(1)若∠ABC=50°,∠ACB=60°,求∠EMF的度数;
(2)若EF=4,求△MEF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,且AC=4
 ,
, 
(1)求AC所在直线的解析式;
(2)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分的面积.
(3)求EF所在的直线的函数解析式.

相关试题

