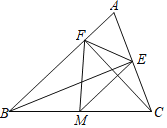
【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,BC=10.
(1)若∠ABC=50°,∠ACB=60°,求∠EMF的度数;
(2)若EF=4,求△MEF的面积.
参考答案:
【答案】(1)∠EMF=40°;(2)2![]() .
.
【解析】
(1)根据直角三角形的性质得到BM=FM,根据等腰三角形的性质、三角形内角和定理计算;
(2)作MN⊥EF于N,根据直角三角形的性质得到FM=![]() BC=5,根据等腰三角形的性质、三角形面积公式计算.
BC=5,根据等腰三角形的性质、三角形面积公式计算.
解:(1)∵CF⊥AB,M为BC的中点,
∴BM=FM,
∵∠ABC=50°,
∴∠MFB=∠MBF=50°,
∴∠BMF=180°-2×50°=80°,
同理,∠CME═180°-2×60°=60°,
∴∠EMF=180°-∠BMF-∠CME=40°;
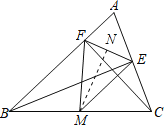
(2)作MN⊥EF于N,
∵CF⊥AB,M为BC的中点,
∴MF是Rt△BFC斜边上的中线,
∴FM=![]() BC=5,
BC=5,
同理可得,ME=5,
∴△EFM是等腰三角形,
∵EF=4,
∴FN=2,
∴MN=![]() =
=![]() ,
,
∴△EFM的面积=![]() EFMN=
EFMN=![]() ×4×
×4×![]() =2
=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组在“用频率估计概率”的实验中,统计了某种频率结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( )

A. 掷一枚质地均匀的硬币,落地时结果是“正面向上”
B. 掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6
C. 在“石头剪刀、和”的游戏中,小明随机出的是“剪刀”
D. 袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)16÷(﹣
 )﹣3﹣(﹣
)﹣3﹣(﹣ )×(﹣4)
)×(﹣4)(2)2(a2b+ab2)﹣2(a2b﹣1)﹣ab2+2
(3)(a﹣b﹣2)(a﹣b+2)
(4)899×901+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】线段AB=12cm,点C在线段AB上,点D、E分别是AC和BC的中点.
(1)若点C恰好是AB中点,求DE的长.
(2)若AC=4cm,求DE的长.
(3)若点C为线段AB上的一个动点(点C不与A,B重合),求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,且AC=4
 ,
, 
(1)求AC所在直线的解析式;
(2)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分的面积.
(3)求EF所在的直线的函数解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(–4,n),B(2,–4)是一次函数y=kx+b的图象和反比例函数
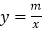 的图象的两个交点.
的图象的两个交点.(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求不等式
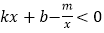 的解集(请直接写出答案).
的解集(请直接写出答案).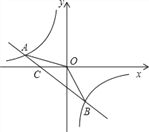
-
科目: 来源: 题型:
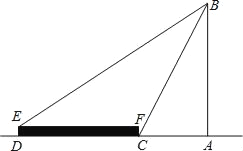
查看答案和解析>>【题目】如图,在一个平台远处有一座古塔,小明在平台底部的点C处测得古塔顶部B的仰角为60°,在平台上的点E处测得古塔顶部的仰角为30°.已知平台的纵截面为矩形DCFE,DE=2米,DC=20米,求古塔AB的高(结果保留根号)
相关试题

