【题目】在平面直角坐标系![]() 中,点
中,点![]() 坐标为
坐标为![]() ,以原点
,以原点![]() 为顶点的四边形
为顶点的四边形![]() 是平行四边形,将边
是平行四边形,将边![]() 沿
沿![]() 轴翻折得到线段
轴翻折得到线段![]() ,连结
,连结![]() 交线段
交线段![]() 于点
于点![]() .
.
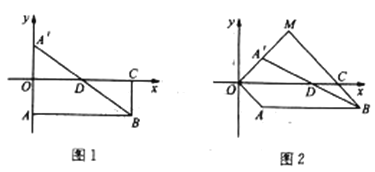
(1)如图1,当点![]() 在
在![]() 轴上,且其坐标为
轴上,且其坐标为![]() .
.
①求![]() 所在直线的函数表达式;
所在直线的函数表达式;
②求证:点![]() 为线段
为线段![]() 的中点;
的中点;
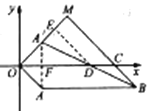
(2)如图2,当![]() 时,
时,![]() ,
,![]() 的延长线相交于点
的延长线相交于点![]() ,试求
,试求![]() 的值.(直接写出答案,不必说明理由)
的值.(直接写出答案,不必说明理由)
参考答案:
【答案】(1)①![]() ;②详见解析;(2)
;②详见解析;(2)![]()
【解析】
(1)①根据四边形![]() 是平行四边形,得
是平行四边形,得![]() ,根据
,根据 ![]() ,
,![]() ,得
,得![]() .根据翻折得到线段
.根据翻折得到线段![]() ,得
,得![]() .设直线
.设直线![]() 的函数表达式为
的函数表达式为![]() ,利用待定系数法确定函数关系式即可求解;
,利用待定系数法确定函数关系式即可求解;
②根据平行四边形的性质求证![]() ,即可得点
,即可得点![]() 为线段
为线段![]() 的中点.
的中点.
(2)连接![]() 交
交![]() 轴于
轴于![]() 点.证明
点.证明![]() 为
为![]() 的中点,得出点
的中点,得出点![]() 为线段
为线段![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,根据平行线分线段成比例定理得到
,根据平行线分线段成比例定理得到![]() ,还可得到等腰直角
,还可得到等腰直角![]() ,故
,故![]() ,求得
,求得![]() .
.
解:(1)①∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() .
.
又∵点![]() 落在
落在![]() 轴上,
轴上,
∴![]() 轴,∴
轴,∴![]() 轴.
轴.
∵![]() ,
,![]() ,∴
,∴![]() .
.
又∵边![]() 沿
沿![]() 轴翻折得到线段
轴翻折得到线段![]() ,
,
∴![]() .
.
设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
∴![]() ,解得
,解得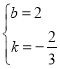 .
.
∴![]() 所在直线的函数表达式为
所在直线的函数表达式为![]() .
.
②证明:∵四边形![]() 是平行四边形,∴
是平行四边形,∴![]() ,
,![]() ,
,
∴![]() .
.
∵边![]() 沿
沿![]() 轴翻折得到线段
轴翻折得到线段![]() ,
,
∴![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() ,
,
∴![]() ,即点
,即点![]() 为线段
为线段![]() 的中点.
的中点.
(2)![]() .
.
连接![]() 交
交![]() 轴于
轴于![]() 点.∴
点.∴![]() 为
为![]() 的中点;
的中点;
∴由(1)可得出点![]() 为线段
为线段![]() 的中点,
的中点,
∵边![]() 沿
沿![]() 轴翻折得到线段
轴翻折得到线段![]() 且
且![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,可得
,可得![]() ,得到等腰直角
,得到等腰直角![]() .
.
∴![]() .
.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形纸片ABCD中,EF∥AB,M,N是线段EF的两个动点,且MN=
 EF,若把该正方形纸片卷成一个圆柱,使点A与点B重合,若底面圆的直径为6cm,则正方形纸片上M,N两点间的距离是____________cm.
EF,若把该正方形纸片卷成一个圆柱,使点A与点B重合,若底面圆的直径为6cm,则正方形纸片上M,N两点间的距离是____________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,搭第一个图形需要
 根火柴棒.
根火柴棒.
(1)搭一搭,填一填:
三角形个数
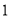
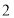
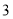

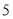
…
火柴棒根数
…
(2)搭
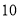 个这样的三角形需要________根火柴棒.
个这样的三角形需要________根火柴棒.(3)搭40个这样的三角形需要________根火柴棒.
(4)搭
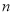 个这样的三角形需要________根火柴棒.
个这样的三角形需要________根火柴棒. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:在四边形中,一条边上的两个角称为邻角.如果一条边上的邻角相等,且这条边对边上的邻角也相等,则把这样的四边形叫做“完美四边形”.
初步运用:在“平行四边形、矩形和菱形”这三种特殊的四边形中,一定是“完美四边形”的是______;
问题探究:在完美四边形
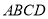 中,
中,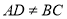 ,
,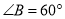 ,
,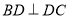 ,
,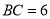 ,求该完美四边形的周长与面积;
,求该完美四边形的周长与面积; -
科目: 来源: 题型:
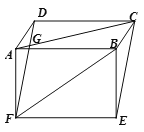
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G.
(1) 试说明DF=CE;
(2) 若AC=BF=DF,求∠ACE的度数.
-
科目: 来源: 题型:
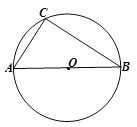
查看答案和解析>>【题目】已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.
(1)求⊙O的半径;
(2)请用尺规作图作出点P,使得点P在优弧CAB上时,△PBC的面积最大,请保留作图痕迹,并求出△PBC面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表.
组别
成绩x分
频数(人数)
第1组
50≤x<60
6
第2组
60≤x<70
8
第3组
70≤x<80
14
第4组
80≤x<90
a
第5组
90≤x<100
10
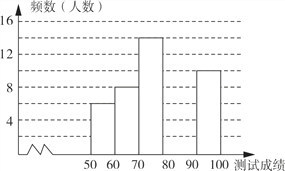
请结合图表完成下列各题:
(1)① 表中a的值为 ;
② 把频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
相关试题

