【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
①写出A、B、C的坐标.
②以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1,并写出A1、B1、C1.

参考答案:
【答案】①A(1,﹣4),B(5,﹣4),C(4,﹣1);②作图参见解析.A1(﹣1,4),B1(﹣5,4),C1(﹣4,1).
【解析】
试题分析:①根据各点所在的象限,对应的横坐标、纵坐标,分别写出点的坐标;②首先根据关于原点对称的点的坐标特点:两个点关于原点对称时,它们的坐标符号相反得到A、B、C的对称点坐标,再顺次连接即可.
试题解析:①根据各点所在的象限,对应的横坐标、纵坐标,分别写出点的坐标:A(1,﹣4),B(5,﹣4),C(4,﹣1);②首先根据两个点关于原点对称时,它们的坐标符号相反得到A、B、C的对称点坐标,再顺次连接即可,如图所示:对应图形写出坐标:A1(﹣1,4),B1(﹣5,4),C1(﹣4,1),

-
科目: 来源: 题型:
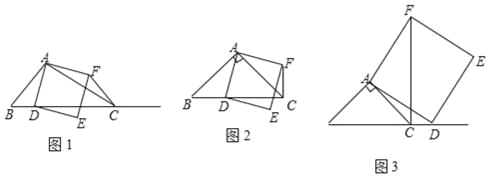
查看答案和解析>>【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,将△ABD绕A点逆时针旋转90°,所得到的三角形为 ,线段CF、BD所在直线的位置关系为 ,线段CF、BD的数量关系为 ;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果P(m+3,2m+4)在y轴上,那么点P的坐标是( )
A.(-2,0)
B.(0,-2)
C.(1,0)
D.(0,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】命题:①对顶角相等;②两直线平行,内错角相等;③全等三角形的对应边相等.其中逆命题为真命题的有几个( )
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长37米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的面积最大?如图是两位学生争议的情境:请根据上面的信息,解决问题:
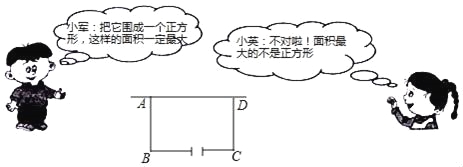
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=-2x+2.
(1)画出它的图象;
(2)求图象与x轴的交点A,与y轴的交点B的坐标;
(3)求A、B两点之间的距离;
(4)观察图象回答,当x为何值时,y≥0?
-
科目: 来源: 题型:
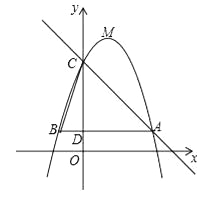
查看答案和解析>>【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(5,3),点C(0,8),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标;
(2)求△ABC的面积;
(3)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.
相关试题

