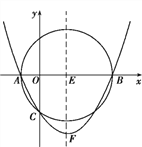
【题目】如图,已知以E(3,0)为圆心,5为半径的☉E与x轴交于A,B两点,与y轴交于C点,抛物线y=ax2+bx+c(a≠0)经过A,B,C三点,顶点为F.
(1)求A,B,C三点的坐标;
(2)求抛物线的解析式及顶点F的坐标;
(3)已知M为抛物线上的一动点(不与C点重合),试探究:①若以A,B,M为顶点的三角形面积与△ABC的面积相等,求所有符合条件的点M的坐标;
②若探究①中的M点位于第四象限,连接M点与抛物线顶点F,试判断直线MF与☉E的位置关系,并说明理由.
参考答案:
【答案】(1)A(-2,0),B(8,0),C(0,-4);(2)抛物线的解析式为y=![]() x2-
x2-![]() x-4,F
x-4,F![]() ;(3)①所点M的坐标为(6,-4),(
;(3)①所点M的坐标为(6,-4),(![]() +3,4),(-
+3,4),(-![]() +3,4);②若M点位于第四象限,则M点即为M1点,此时直线MF和☉E相切,理由见解析.
+3,4);②若M点位于第四象限,则M点即为M1点,此时直线MF和☉E相切,理由见解析.
【解析】分析:(1)由题意可直接得到点A、B的坐标,连接CE,在Rt△OCE中,利用勾股定理求出OC的长,则得到点C的坐标;
(2)已知点A、B、C的坐标,利用交点式与待定系数法求出抛物线的解析式,由解析式得到顶点F的坐标;
(3)①△ABC中,底边AB上的高OC=4,若△ABC与△ABM面积相等,则抛物线上的点M须满足条件:|yM|=4.因此解方程yM=4和yM=-4,可求得点M的坐标;
②如解答图,作辅助线,可求得EM=5,因此点M在 E上;再利用勾股定理求出MF的长度,则利用勾股定理的逆定理可判定△EMF为直角三角形,∠EMF=90°,所以直线MF与 E相切.
详解:(1)由题图可得点A的横坐标为3-5=-2,点B的横坐标为3+5=8,
连接CE,则CE=5,又OE=3,
∴OC=![]() =4,
=4,
∴A(-2,0),B(8,0),C(0,-4).
(2)把(-2,0),(8,0),(0,-4)代入y=ax2+bx+c,得.
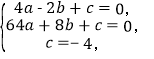 解得
解得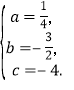
∴抛物线的解析式为y=![]() x2-
x2-![]() x-4.
x-4.
∵EF∥y轴,∴点F的横坐标为3.
把x=3代入y=![]() x2-
x2-![]() x-4,得y=-
x-4,得y=-![]() ,
,
∴F![]() .
.
(3)①如图所示,连接AC,BM1,BC,
易知![]() =S△ABC,△ABM1与△ABC同底等高,
=S△ABC,△ABM1与△ABC同底等高,
点C与点M1关于直线x=3对称,
M1(6,-4).
把y=4代入y=![]() x2-
x2-![]() x-4,得
x-4,得![]() x2-
x2-![]() x-4=4,
x-4=4,
解得x1=![]() +3,x2=-
+3,x2=-![]() +3,
+3,
∴M2(![]() +3,4),M3(-
+3,4),M3(-![]() +3,4).
+3,4).
∴所有符合条件的点M的坐标为(6,-4),(![]() +3,4),(-
+3,4),(-![]() +3,4).
+3,4).
②若M点位于第四象限,则M点即为M1点,此时直线MF和☉E相切.
理由如下:M1(6,-4),圆心E(3,0),点F![]() ,
,
连接M1E.
利用勾股定理得M1E=5,M1F=![]() ,又EF=
,又EF=![]() ,
,
∴M1E2+M1F2=EF2,即∠FM1E=90°,
∴M1E⊥M1F.
∵M1E是☉E的半径,
∴直线M1F和☉E相切,
即当M点位于第四象限时,直线MF与☉E相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解该校学生的课余活动情况,采用抽样调查的方式,从运动、娱乐、阅读和其他四个方面调查了若干名学生的兴趣和爱好情况,并根据调查结果制作了如下两幅统计图.

根据图中提供的信息解答下列问题:
(1)求本次抽样调查的人数;(要求列式计算,写出求解过程)
(2)补全人数统计图;
(3)“运动”对应的扇形的圆心角度数是 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,每个小方格都是边长为
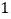 的正方形,
的正方形,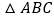 的顶点均在格点上,点
的顶点均在格点上,点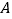 的坐标是
的坐标是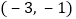 .
.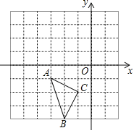
 先将
先将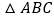 沿
沿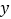 轴正方向向上平移
轴正方向向上平移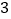 个单位长度,再沿
个单位长度,再沿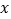 轴负方向向左平移
轴负方向向左平移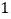 个单位长度得到
个单位长度得到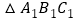 ,画出
,画出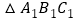 ,点
,点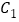 坐标是________;
坐标是________;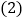 将
将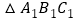 绕点
绕点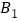 逆时针旋转
逆时针旋转 ,得到
,得到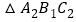 ,画出
,画出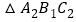 ,并求出点
,并求出点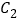 的坐标是________;
的坐标是________;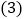 我们发现点
我们发现点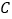 、
、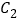 关于某点中心对称,对称中心的坐标是________.
关于某点中心对称,对称中心的坐标是________. -
科目: 来源: 题型:
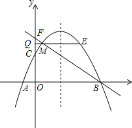
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,2),点M(m,n)是抛物线上一动点,位于对称轴的左侧,并且不在坐标轴上,过点M作x轴的平行线交y轴于点Q,交抛物线于另一点E,直线BM交y轴于点F.
(1)求抛物线的解析式,并写出其顶点坐标;
(2)当S△MFQ:S△MEB=1:3时,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多边形上或内部的一点与多边形各顶点的连线,可以将多边形分割成若干个小三角形.如图,给出了四边形的三种具体分割方法,分别将四边形分割成了2个、3个、4个小三角形,这样我们就可以借助研究三角形的经验研究四边形了.
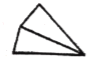
图①被分割成2个小三角形

图②被分割成3个小三角形

图③被分割成4个小三角形
(1)请按照上述三种方法分别将图中的六边形进行分割,并写出每种方法所得到的小三角形的个数:
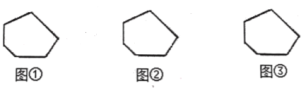
图①被分割成 个小三角形、图②被分割成 个小三角形、图③被分割成 个小三角形;
(2)如果按照上述三种分割方法分别分割
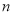 边形,请写出每种方法所得到的小三角形的个数(用含
边形,请写出每种方法所得到的小三角形的个数(用含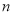 的代数式写出结论即可,不必画图):按照上述图①、图②、图③的分割方法,
的代数式写出结论即可,不必画图):按照上述图①、图②、图③的分割方法,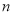 边形分别可以被分割成 、 、 个小三角形.
边形分别可以被分割成 、 、 个小三角形. -
科目: 来源: 题型:
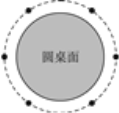
查看答案和解析>>【题目】元旦那天,6位朋友均匀地围坐在圆桌旁共度佳节.如图,圆桌半径为60 cm,每人离圆桌的距离均为10 cm,现又来了两名客人,每人向后挪动了相同的距离,再左右调整位置,使8人都坐下,并且8人之间的距离与原来6人之间的距离(即在圆周上两人之间的圆弧的长)相等.设每人向后挪动的距离为x,根据题意,可列方程( ).
A.
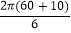 =
=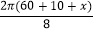
B.
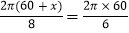
C. 2π(60+10)×6=2π(60+π)×8
D. 2π(60-x)×8=2π(60+x)×6
相关试题

