【题目】如图,已知数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,
,![]() 是数轴上一点,且
是数轴上一点,且![]() ,动点
,动点![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向左匀速运动,设运动时间为
个单位长度的速度沿数轴向左匀速运动,设运动时间为![]() 秒.
秒.
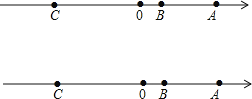
(1)直接写出数轴上点![]() 表示的数,并用含
表示的数,并用含![]() 的代数式表示线段
的代数式表示线段![]() 的长度;
的长度;
(2)设![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点.点
的中点.点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若变化,请说出理由;若不变,求线段
的长度是否发生变化?若变化,请说出理由;若不变,求线段![]() 的长度.
的长度.
(3)动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向左匀速运动,动点
个单位长度的速度沿数轴向左匀速运动,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度沿数轴向左匀速运动,若
个单位长度沿数轴向左匀速运动,若![]() 三点同时出发,当点
三点同时出发,当点![]() 追上点
追上点![]() 后立即返回向点
后立即返回向点![]() 运动,遇到点
运动,遇到点![]() 后则停止运动.求点
后则停止运动.求点![]() 从开始运动到停止运动,行驶的路程是多少个单位长度?
从开始运动到停止运动,行驶的路程是多少个单位长度?
参考答案:
【答案】(1)![]() 点表示的数为
点表示的数为![]() ,线段
,线段![]() 的长度为
的长度为![]() ;(2)线段
;(2)线段![]() 的长度不发生变化,其值为
的长度不发生变化,其值为![]() ;(3)
;(3)![]() 从开始运动到停止运动,行驶的路程是
从开始运动到停止运动,行驶的路程是![]() 个单位长度.
个单位长度.
【解析】
(1)![]() 点表示的数为
点表示的数为![]() ,线段
,线段![]() 的长度为
的长度为![]() ;
;
(2)分类讨论:①当点![]() 在点
在点![]() 两点之间运动时;②当点
两点之间运动时;②当点![]() 运动到点
运动到点![]() 的左侧时;利用中点的定义和线段的和差易求出
的左侧时;利用中点的定义和线段的和差易求出![]() ;
;
(3)先求出![]() 从
从![]() 出发相遇时的时间,再求出
出发相遇时的时间,再求出![]() 相遇时
相遇时![]() 之间剩余的路程的相遇时间,就可以求出
之间剩余的路程的相遇时间,就可以求出![]() 一共走的时间,由
一共走的时间,由![]() 的速度就可以求出
的速度就可以求出![]() 点行驶的路程.
点行驶的路程.
解:(1)设![]() 点表示的数为
点表示的数为![]() ,由题意,得
,由题意,得
![]() ,
,
解得![]() .
.
故![]() 点表示的数为
点表示的数为![]() ,线段
,线段![]() 的长度为
的长度为![]() ;
;
(2)线段![]() 的长度不发生变化.
的长度不发生变化.
理由:分两种情况:
①当点![]() 在
在![]() 两点之间运动时,如图:
两点之间运动时,如图:
![]()
![]()
②当点![]() 运动到点
运动到点![]() 的左边时,如图:
的左边时,如图:
![]()
![]()
综上所述,线段![]() 的长度不发生变化,其值为
的长度不发生变化,其值为![]() .
.
(3)由题意得:
![]() 的相遇时间为:
的相遇时间为:![]() ,
,
![]() 剩余的路程为:
剩余的路程为:![]() 个单位长度,
个单位长度,
![]() 相遇的时间为:
相遇的时间为:![]()
![]() 点走的路程为:
点走的路程为:![]() 个单位长度.
个单位长度.
故点![]() 从开始运动到停止运动,行驶的路程是
从开始运动到停止运动,行驶的路程是![]() 个单位长度.
个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请观察下列算式,找出规律并填空
 =1-
=1- ,
,  =
= -
- ,
,  =
= -
- ,
,  =
= -
-
则第10个算式是 _____________=_____________
第n个算式是 ___________=_____________
根据以上规律解答以下三题:(1)

(2)若有理数a、b满足|a-1|+
 =0 ,试求:
=0 ,试求: +
+ +
+ + …+
+ …+ 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在学校组织的八年级知识竞赛中,每班参加比赛的人数相同,成绩分为
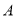 、
、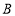 、
、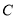 、
、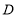 四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将一班和二班的成绩整理并绘制成如下的统计图:
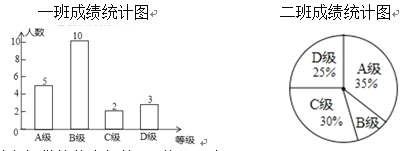
四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将一班和二班的成绩整理并绘制成如下的统计图:请你根据以上提供的信息解答下列问题:
(1)求一班参赛选手的平均成绩;
(2)此次竞赛中,二班成绩在
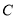 级以上(包括
级以上(包括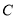 级)的人数有几人?
级)的人数有几人?(3)求二班参赛选手成绩的中位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进
 、
、 两种新型节能台灯共
两种新型节能台灯共 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:
(
 )若商场预计进货款为
)若商场预计进货款为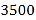 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?(
 )若商场规定
)若商场规定 型台灯的进货数量不超过
型台灯的进货数量不超过 型台灯数量的
型台灯数量的 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元? -
科目: 来源: 题型:
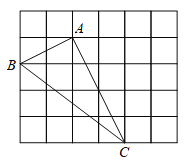
查看答案和解析>>【题目】如图,在由边长为1的小正方形组成的网格中,
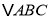 的三个顶点均在格点上,请解答:
的三个顶点均在格点上,请解答:(1)判断
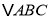 的形状,并说明理由;
的形状,并说明理由; (2)在网格图中画出AD//BC,且AD=BC;
(3)连接CD,若E为BC中点,F为AD中点,四边形AECF是什么特殊的四边形?请说明理由.
-
科目: 来源: 题型:
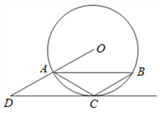
查看答案和解析>>【题目】如图,△ABC内接于⊙O,CA=CB,CD∥AB,CD与OA的延长线交于点D.
(1)求证:CD 是⊙O 的切线;
(2)若∠ACB=120°,OA=2,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)

(2)
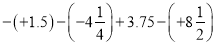
(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

相关试题

