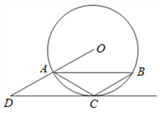
【题目】如图,△ABC内接于⊙O,CA=CB,CD∥AB,CD与OA的延长线交于点D.
(1)求证:CD 是⊙O 的切线;
(2)若∠ACB=120°,OA=2,求CD的长.
参考答案:
【答案】(1)证明见解析(2) ![]()
【解析】试题分析:(1)连接OC,证明OC⊥DC,利用经过半径的外端且垂直于半径的直线是圆的切线判定切线即可;
(2)利用等弧所对的圆心角相等和题目中的已知角得到∠D=30°,利用解直角三角形求得CD的长即可;
试题解析:解:(1)CD与⊙O相切.理由如下:
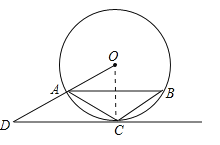
如图,连接OC.∵CA=CB,∴弧AC=弧CB,∴OC⊥AB.∵CD∥AB,∴OC⊥CD.∵OC是半径,∴CD与⊙O相切.
(2)∵CA=CB,∠ACB=120°,∴∠ABC=30°,∴∠DOC=60°,∴∠D=30°,∴OC=![]() OD.∵OA=OC=2,∴DO=4,∴CD=
OD.∵OA=OC=2,∴DO=4,∴CD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进
 、
、 两种新型节能台灯共
两种新型节能台灯共 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:
(
 )若商场预计进货款为
)若商场预计进货款为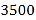 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?(
 )若商场规定
)若商场规定 型台灯的进货数量不超过
型台灯的进货数量不超过 型台灯数量的
型台灯数量的 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点
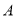 表示的数为
表示的数为 ,点
,点 表示的数为
表示的数为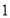 ,
,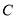 是数轴上一点,且
是数轴上一点,且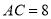 ,动点
,动点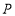 从
从 出发,以每秒
出发,以每秒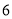 个单位长度的速度沿数轴向左匀速运动,设运动时间为
个单位长度的速度沿数轴向左匀速运动,设运动时间为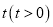 秒.
秒.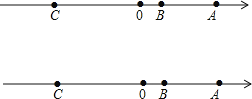
(1)直接写出数轴上点
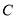 表示的数,并用含
表示的数,并用含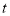 的代数式表示线段
的代数式表示线段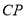 的长度;
的长度;(2)设
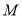 是
是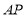 的中点,
的中点,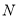 是
是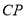 的中点.点
的中点.点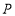 在运动过程中,线段
在运动过程中,线段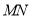 的长度是否发生变化?若变化,请说出理由;若不变,求线段
的长度是否发生变化?若变化,请说出理由;若不变,求线段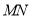 的长度.
的长度.(3)动点
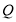 从点
从点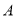 出发,以每秒
出发,以每秒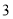 个单位长度的速度沿数轴向左匀速运动,动点
个单位长度的速度沿数轴向左匀速运动,动点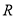 从点
从点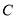 出发,以每秒
出发,以每秒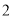 个单位长度沿数轴向左匀速运动,若
个单位长度沿数轴向左匀速运动,若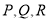 三点同时出发,当点
三点同时出发,当点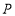 追上点
追上点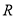 后立即返回向点
后立即返回向点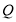 运动,遇到点
运动,遇到点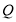 后则停止运动.求点
后则停止运动.求点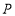 从开始运动到停止运动,行驶的路程是多少个单位长度?
从开始运动到停止运动,行驶的路程是多少个单位长度? -
科目: 来源: 题型:
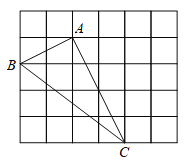
查看答案和解析>>【题目】如图,在由边长为1的小正方形组成的网格中,
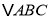 的三个顶点均在格点上,请解答:
的三个顶点均在格点上,请解答:(1)判断
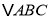 的形状,并说明理由;
的形状,并说明理由; (2)在网格图中画出AD//BC,且AD=BC;
(3)连接CD,若E为BC中点,F为AD中点,四边形AECF是什么特殊的四边形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)

(2)
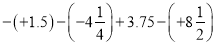
(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

-
科目: 来源: 题型:
查看答案和解析>>【题目】杭州休博会期间,嘉年华游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收33万元.而该游乐设施开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx;若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数;
(1)若维修保养费用第1个月为2万元,第2个月为4万元.求y关于x的解析式;
(2)求纯收益g关于x的解析式;
(3)问设施开放几个月后,游乐场的纯收益达到最大;几个月后,能收回投资?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
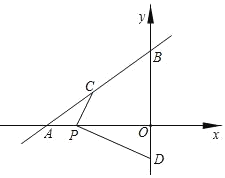
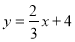 与x轴、y轴分别交于点A和点B,点C在线段AB上,点D在y轴的负半轴上,C、D两点到x轴的距离均为2.
与x轴、y轴分别交于点A和点B,点C在线段AB上,点D在y轴的负半轴上,C、D两点到x轴的距离均为2.(1)点C的坐标为 ,点D的坐标为 ;
(2)点P为线段OA上的一动点,当PC+PD最小时,求点P的坐标.
相关试题

