【题目】已知三角形两条边的长分别为2、4,则第三条边的长可以是( )
A.1
B.3
C.6
D.7
参考答案:
【答案】B
【解析】解:2+4=6,4﹣2=2,所以第三边在2到6之间.只有B中的3满足. 故选B.
【考点精析】通过灵活运用三角形三边关系,掌握三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市24000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:
分数段
频数
频率
x<60
20
0.10
60≤x<70
28
0.14
70≤x<80
54
0.27
80≤x<90
a
0.20
90≤x<100
24
0.12
100≤x<110
18
b
110≤x<120
16
0.08
请根据以上图表提供的信息,解答下列问题:
(1)表中a和b所表示的数分别为多少;
(2)请在图中,补全频数分布直方图;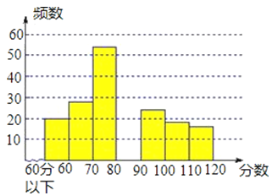
(3)如果把成绩在90分以上(含90分)定为优秀,那么该市24000名九年级考生数学成绩为优秀的学生约有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走:
(1)假如每天能运x立方米,所需时间为y天,写出y与x之间的函数表达式;
(2)若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,E,F分别是BC,AC的中点,延长BA到点D,使AD=
 AB.连接DE,DF.
AB.连接DE,DF.
(1)求证:AF与DE互相平分;
(2)若BC=4,求DF的长.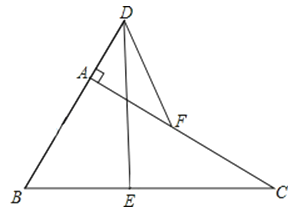
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式由左边到右边的变形,是因式分解的是( )
A.3x(x+y)+3x2+3xy
B.﹣2x2﹣2xy=﹣2x(x+y)
C.(x+5)(x﹣5)=x2﹣25
D.x2+x+1=x(x+1)+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
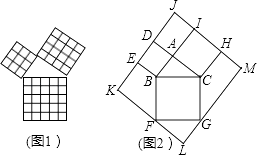
A.90
B.100
C.110
D.121 -
科目: 来源: 题型:
查看答案和解析>>【题目】若(mx4)·(4xk)=-12x12,则适合条件的m,k的值分别是( )
A. m=-3,k=8 B. m=3,k=8
C. m=8,k=3 D. m=-3,k=3
相关试题

