【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为( ) 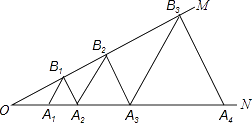
A.6
B.12
C.32
D.64
参考答案:
【答案】C
【解析】解:∵△A1B1A2是等边三角形, ∴A1B1=A2B1 , ∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,
∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=1,
∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3 , B1A2∥B2A3 ,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2 , B3A3=2B2A3 ,
∴A3B3=4B1A2=4,
A4B4=8B1A2=8,
A5B5=16B1A2=16,
以此类推:A6B6=32B1A2=32.
故选:C.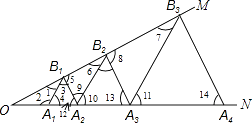
【考点精析】利用等边三角形的性质和含30度角的直角三角形对题目进行判断即可得到答案,需要熟知等边三角形的三个角都相等并且每个角都是60°;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】情境观察:
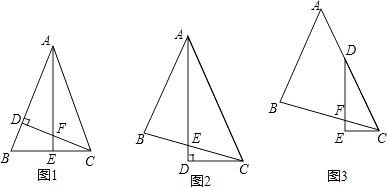
(1)如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形;
②线段AF与线段CE的数量关系是 .
(2)问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
(3)拓展延伸:
如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC= ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果x2﹣(m+1)x+1是完全平方式,则m的值为( )
A.-1
B.1
C.1或﹣1
D.1或﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列线段能构成三角形的是( )
A.2,2,4 B.3,4,5 C.1,2,3 D.2,3,6
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知线段AB的两个端点分别是A(﹣4,﹣1),B(1,1),将线段AB平移后得到线段A′B′,若点A′的坐标为(﹣2,2),则点B′的坐标为( )
A.(4,3)
B.(3,4)
C.(﹣1,﹣2)
D.(﹣2,﹣1) -
科目: 来源: 题型:
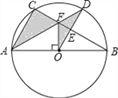
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2
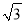 .
.(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的周长为18cm,其中一条边为4cm,那么等腰三角形的底边长为_________
相关试题

