【题目】如图,正方形OABC的边长为3,点A、C分别在x轴,y轴的正半轴上,点D(1,0)在OA上,P是OB上一动点,则PA+PD的最小值为_____.

参考答案:
【答案】![]() .
.
【解析】
过D点作关于OB的对称点D′,连接D′A交OB于点P,由两点之间线段最短可知D′A即为PA+PD的最小值,
由正方形的性质可求出D′点的坐标,再根据OA=3可求出A点的坐标,利用两点间的距离公式即可求出D′A的值.
解:过D点作关于OB的对称点D′,连接D′A交OB于点P,由两点之间线段最短可知D′A即为PA+PD的最小值,
∵D(1,0),四边形OABC是正方形,
∴D′点的坐标为(0,1),A点坐标为(3,0),
∴D′A=![]() =
=![]() ,即PA+PD的最小值为
,即PA+PD的最小值为![]() .
.
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( )

A. 6
 B. 6C. 3
B. 6C. 3 D. 3+3
D. 3+3
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数的计算:
(1)1﹣(﹣8)+12+(﹣11);
(2)|﹣
 |
| ;
;(3)﹣12﹣(1﹣
 )
) ×[6+(﹣3)3];
×[6+(﹣3)3];(4)
 ×(﹣6)2﹣5.5×8+25.5×8.
×(﹣6)2﹣5.5×8+25.5×8. -
科目: 来源: 题型:
查看答案和解析>>【题目】将形状、大小完全相同的两个等腰三角形如图所示放置,点D在AB边上,△DEF绕点D旋转,腰DF和底边DE分别交△CAB的两腰CA,CB于M,N两点,若CA=5,AB=6,AD:AB=1:3,则MD+
 的最小值为 .
的最小值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)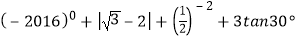 ;
;
(2)先化简 ,再选一个你喜欢的数求值.
,再选一个你喜欢的数求值.
(1)(﹣2016)0+| ﹣2|+
﹣2|+  +3tan30°
+3tan30°
(2)先化简(a2﹣a)÷ ,再选一个你喜欢的数求值.
,再选一个你喜欢的数求值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AC=BC=5,AB=5
 ,三角形顶点在相互平行的三条直线L1,L2,L3上,且L2,L3之间的距离为3,则L1,L3之间的距离是_____.
,三角形顶点在相互平行的三条直线L1,L2,L3上,且L2,L3之间的距离为3,则L1,L3之间的距离是_____.
-
科目: 来源: 题型:
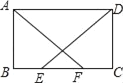
查看答案和解析>>【题目】如图,在ABCD中,E、F为边BC上两点,且BE=CF,AF=DE.
(1)求证:△ABF≌△DCE;
(2)四边形ABCD是矩形吗?为什么?
相关试题

