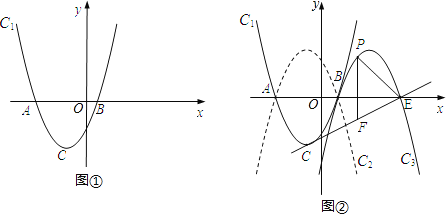
【题目】如图①,已知抛物线C1:y=a(x+1)2﹣4的顶点为C,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
(1)求点C的坐标及a 的值;
(2)如图②,抛物线C2与C1关于x轴对称,将抛物线C2向右平移4个单位,得到抛物线C3.C3与x轴交于点B、E,点P是直线CE上方抛物线C3上的一个动点,过点P作y轴的平行线,交CE于点F.
①求线段PF长的最大值;
②若PE=EF,求点P的坐标.
参考答案:
【答案】(1)a=1;顶点C为(﹣1,﹣4).(2)①当x=![]() 时,PF有最大值为
时,PF有最大值为![]() ;②P(
;②P(![]() ,
,![]() ).
).
【解析】
试题分析:(1)根据二次函数的性质即可直接求得顶点C的坐标,把B的坐标代入函数解析式即可求得a的值;
(2)①C2的顶点坐标是C关于x轴的对称点,且二次项系数互为相反数,据此即可求得C2的解析式,然后根据平移的性质求得C3的解析式.利用待定系数法求得直线CE的解析式,则PF的长即可利用x表示出来,然后根据二次函数的性质求得PF的最大值;
②PE=EF则P和F关于x轴对称,即纵坐标互为相反数,据此即可列方程求解.
解:(1)顶点C为(﹣1,﹣4).
∵点B(1,0)在抛物线C1上,∴0=a(1+1)2﹣4,解得,a=1;
(2)①∵C2与C1关于x轴对称,
∴抛物线C2的表达式为y=﹣(x+1)2+4,
抛物线C3由C2平移得到,
∴抛物线C3为y=﹣(x﹣3)2+4=﹣x2+6x﹣5,
∴E(5,0),
设直线CE的解析式为:y=kx+b,
则![]() ,解得
,解得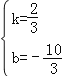 ,
,
∴直线BC的解析式为y=![]() x﹣
x﹣![]() ,
,
设P(x,﹣x2+6x﹣5),则F(x,![]() x﹣
x﹣![]() ),
),
∴PF=(﹣x2+6x﹣5)﹣(![]() x﹣
x﹣![]() )=﹣x2+
)=﹣x2+![]() x﹣
x﹣![]() =﹣(x﹣
=﹣(x﹣![]() )2+
)2+![]() ,
,
∴当x=![]() 时,PF有最大值为
时,PF有最大值为![]() ;
;
②若PE=EF,∵PF⊥x轴,
∴x轴平分PF,
∴﹣x2+6x﹣5=﹣![]() x+
x+![]() ,
,
解得x1=![]() ,x2=5(舍去)
,x2=5(舍去)
∴P(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要设计一本画册的封面,封面长40cm,宽30cm,正中央是一个与整个封面长宽比例相同的矩形画.如果要使四周的边衬所占面积是封面面积的
 ,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位,参考数据:
,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位,参考数据: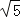 ≈2.236).
≈2.236).
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明“a<b”时应假设( )
A. a>b B. a≤b C. a=b D. a≥b
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程x2﹣3x+k=0有一个根是﹣1,则该方程的另一根是( ).
A.1 B.0 C.﹣4 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于距发射架底部4km处的地面雷达站R(LR=4)测得火箭底部的仰角为43°.1s后,火箭到达B点,此时测得火箭底部的仰角为45.72°.这枚火箭从A到B的平均速度是多少 (结果取小数点后两位)?
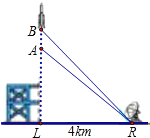
(参考数据:sin43°≈0.682,cos43°≈0.731,tan43°≈0.933,
sin45.72°≈0.716,cos45.72°≈0.698,tan45.72°≈1.025)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两地相距40千米,中午12:00时,甲从A地出发开车到B地,12:10时乙从B地出发骑自行车到A地,设甲行驶的时间为t(分),甲、乙两人离A地的距离S(千米)与时间t(分)之间的关系如图所示.由图中的信息可知,乙到达A地的时间为( )
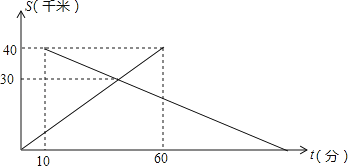
A.14:00 B.14:20 C.14:30 D.14:40
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.

相关试题

