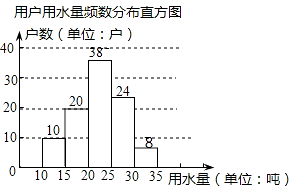
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是 .
(2)补全频数分布直方图.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
参考答案:
【答案】
(1)100
(2)解:“15吨﹣20吨”部分的户数为100﹣(10+38+24+8)=20(户),
补全图形如下:
(3)解:6× ![]() =4.08(万户),
=4.08(万户),
答:该地区6万用户中约有4.08万用户的用水全部享受基本价格
【解析】解:(1)此次抽样调查的总户数是10÷10%=100(户),
所以答案是:100;
【考点精析】本题主要考查了总体、个体、样本、样本容量和频数分布直方图的相关知识点,需要掌握所要考察的全体对象叫总体,组成总体的每一个考察对象叫个体,被抽取的那部分个体组成总体的一个样本,样本中个体的数目叫这个样本的容量(样本容量没有单位);特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB、BC于点E、F、G,连接ED、DG.
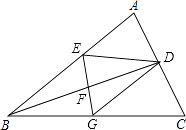
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2,求GC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△CED均为等边三角形,且B,C,D三点共线.线段BE,AD相交于点O,AF⊥BE于点F.若OF=1,则AF的长为( )
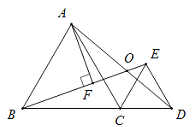
A. 1 B.
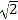 C.
C. 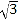 D. 2
D. 2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
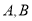 的坐标分别是点
的坐标分别是点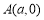 ,
, ,且
,且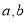 满足:
满足: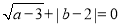 .
.(1)则
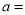 _________,
_________,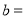 _________;
_________;(2)
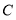 为
为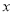 轴负半轴上一点,过点
轴负半轴上一点,过点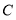 作
作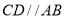 交
交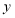 轴于点
轴于点 .
.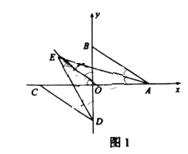
①如图1,
 与
与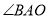 的角平分线交于点
的角平分线交于点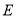 ,求
,求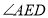 的度数;
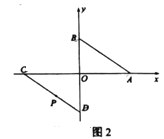
的度数;②如图2,点
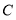 的坐标为
的坐标为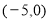 ,点
,点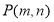 为线段
为线段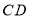 上一点,求
上一点,求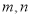 之间满足的关系式.
之间满足的关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂准备翻建新的大门,厂门要求设计成轴对称的拱形曲线.已知厂门的最大宽度AB=12m,最大高度OC=4m,工厂的运输卡车的高度是3m,宽度是5.8m.现设计了两种方案.方案一:建成抛物线形状(如图1);方案二:建成圆弧形状(如图2).为确保工厂的卡车在通过厂门时更安全,你认为应采用哪种设计方案?请说明理由.
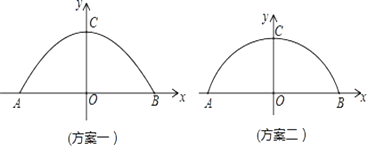
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
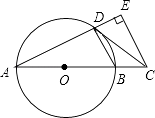
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
相关试题

