【题目】把顺序连结四边形各边中点所得的四边形叫中点四边形。
(1)任意四边形的中点四边形是什么形状?为什么?
(2)符合什么条件的四边形,它的中点四边形是菱形?
(3)符合什么条件的四边形,它的中点四边形是矩形?
参考答案:
【答案】(1)平行四边形;理由见解析;(2)当原四边形的对角线相等时,它的中点四边形是菱形;(3)当原四边形的对角线互相垂直时,它的中点四边形是矩形.
【解析】
(1)连接BD、由点E、H分别为边AB、AD的中点,同理知FG∥BD、FG=![]() BD,据此可得EH=FG、EH∥FG,即可得证;
BD,据此可得EH=FG、EH∥FG,即可得证;
(2)同理根据对角线相等,可知邻边相等,中点四边形是菱形;
(3)同理根据对角线互相垂直,可知有一个角是直角,中点四边形是矩形.
(1)任意四边形的中点四边形是平行四边形,理由是:
如图1,连接BD,
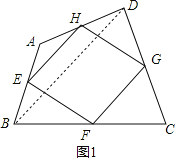
∵点E、H分别为边AB、AD的中点,
∴EH∥BD、EH=![]() BD,
BD,
∵点F、G分别为BC、DC的中点,
∴FG∥BD、FG=![]() BD,
BD,
∴EH=FG、EH∥FG,
∴中点四边形EFGH是平行四边形;
(2)当原四边形的对角线相等时,它的中点四边形是菱形;
证明:与(1)同理:EH=FG=![]() BD=
BD=![]() AC=EF=HG,得它的中点四边形是菱形;
AC=EF=HG,得它的中点四边形是菱形;
(3)当原四边形的对角线互相垂直时,它的中点四边形是矩形;
证明:与(1)同理:EH∥FG∥BD,AC∥EF∥HG,
∵AC⊥BD,
∴EH、FG分别与EF、HG垂直,
∴得它的中点四边形是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小王某天下午营运的路线全是在东西走向的大道上,小王从点
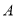 出发,如果规定向东为正,向西为负,他这天下午的行驶记录如下:+5,-3,-8,-6,+10,-6,+12,-10(单位:千米)
出发,如果规定向东为正,向西为负,他这天下午的行驶记录如下:+5,-3,-8,-6,+10,-6,+12,-10(单位:千米)(1)将最后一名乘客送到目的地时,小王距离出发点
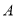 是多少千米?在点
是多少千米?在点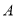 的哪个方向?
的哪个方向?(2)若汽车耗油量为
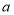 升/千米,小王送完最后一个乘客后回到出发点
升/千米,小王送完最后一个乘客后回到出发点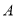 ,共耗油多少升?(用含
,共耗油多少升?(用含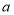 的代数式表示)
的代数式表示)(3)出租车油箱内原有12升油,请问:当
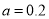 时,小王途中是否需要加油?若需要加油,至少需要加多少升油?如不需要,说明理由.
时,小王途中是否需要加油?若需要加油,至少需要加多少升油?如不需要,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点
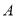 表示数
表示数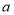 ,点
,点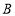 表示数
表示数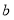 ,点
,点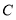 表示数
表示数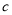 ,且点
,且点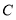 在点
在点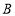 的左侧,同时
的左侧,同时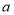 、
、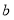 满足
满足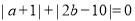 ,
,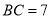 .
.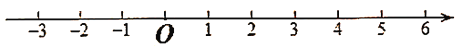
(1)由题意:
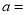 ______,
______,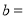 ______,
______,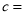 ______;
______;(2)当点
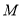 在数轴上运动时,点
在数轴上运动时,点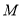 到
到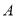 、
、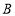 两点距离之和的最小值为______.
两点距离之和的最小值为______.(3)动点
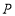 、
、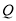 分别从点
分别从点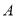 、
、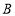 沿数轴负方向匀速运动同时出发,点
沿数轴负方向匀速运动同时出发,点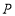 的速度是每秒
的速度是每秒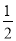 个单位长度,点
个单位长度,点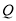 的速度是每秒2个单位长度,求运动几秒后,
的速度是每秒2个单位长度,求运动几秒后,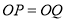 ?
?(4)在数轴上找一点
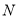 ,使点
,使点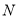 到
到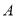 、
、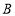 、
、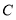 三点的距离之和等于10,请直接写出所有的点
三点的距离之和等于10,请直接写出所有的点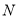 对应的数.(不必说明理由)
对应的数.(不必说明理由) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是AB的中点,点D是BC的中点,现给出下列等式:①CD=AC-DB,②CD=
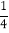 AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )
AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )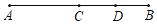
A.
 B.
B.  C.
C. 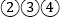 D.
D. 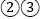
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=
 (x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
(x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.(1)求点D的坐标;
(2)点F是OC边上一点,若△FBC和△DEB相似,求点F的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明在数学课外小组活动时遇到这样一个问题:
如果一个不等式(含有不等号的式子)中含有绝对值,并且绝对值符号中含有未知数,我们把这个不等式叫做绝对值不等式.
求绝对值不等式
 的解集(满足不等式的所有解).
的解集(满足不等式的所有解).小明同学的思路如下:
先根据绝对值的定义,求出
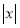 恰好是3时
恰好是3时 的值,并在数轴上表示为点
的值,并在数轴上表示为点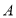 ,
, ,如图所示.观察数轴发现,
,如图所示.观察数轴发现,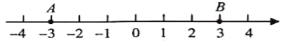
以点
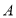 ,
,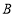 为分界点把数轴分为三部分:
为分界点把数轴分为三部分:点
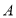 左边的点表示的数的绝对值大于3;
左边的点表示的数的绝对值大于3;点
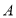 ,
,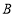 之间的点表示的数的绝对值小于3;
之间的点表示的数的绝对值小于3;点B右边的点表示的数的绝对值大于3.
因此,小明得出结论,绝对值不等式
 的解集为:
的解集为: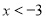 或
或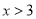 .
.参照小明的思路,解决下列问题:
(1)请你直接写出下列绝对值不等式的解集.
①
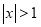 的解集是 ;
的解集是 ;②
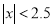 的解集是 .
的解集是 .(2)求绝对值不等式
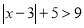 的解集.
的解集.(3)直接写出不等式
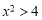 的解集是 .
的解集是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个有两个圆柱形构成的容器,最下面的圆柱形底面半径
 。匀速地向空容器内注水,水面高度
。匀速地向空容器内注水,水面高度 (单位:米)与时间
(单位:米)与时间 (单位:小时)的关系如图2所示。
(单位:小时)的关系如图2所示。
(1)求水面高度
 与时间
与时间 的函数关系式;
的函数关系式;(2)求注水的速度(单位:立方米/每小时),并求容器内水的体积
 与注水时间
与注水时间 的函数关系式;
的函数关系式;(3)求上面圆柱的底面半径(壁厚忽略不计)。
相关试题

