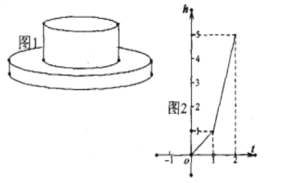
【题目】如图1是一个有两个圆柱形构成的容器,最下面的圆柱形底面半径![]() 。匀速地向空容器内注水,水面高度
。匀速地向空容器内注水,水面高度![]() (单位:米)与时间
(单位:米)与时间![]() (单位:小时)的关系如图2所示。
(单位:小时)的关系如图2所示。

(1)求水面高度![]() 与时间
与时间![]() 的函数关系式;
的函数关系式;
(2)求注水的速度(单位:立方米/每小时),并求容器内水的体积![]() 与注水时间
与注水时间![]() 的函数关系式;
的函数关系式;
(3)求上面圆柱的底面半径(壁厚忽略不计)。
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)4
;(3)4
【解析】
(1)由待定系数法可求水面高度h与时间t的函数关系式;
(2)由下面的圆柱形的体积=注水的速度×时间,可列方程,求出注水速度,即可求容器内水的体积V与注水时间t的函数关系式;
(3)由上面的圆柱形的体积=注水的速度×时间,可列方程,求解即可.
(1)当0≤t≤1时,设水面高度h与时间t的函数关系式:h=kt,且过(1,1)
∴1=k
∴当0≤t≤1时,设水面高度h与时间t的函数关系式:h=t
当1<t≤2时,设水面高度h与时间t的函数关系式:h=mt+n,且过(1,1),(2,5)
∴![]()
解得:![]()
∴当1<t≤2时,设水面高度h与时间t的函数关系式:h=4t-3
所以水面高度![]() 与时间
与时间![]() 的函数关系是
的函数关系是![]()
(2)由图2知,注满下面圆柱所花的时间是![]() 小时,下面圆柱的高度是
小时,下面圆柱的高度是![]() 米,设注水的速度为
米,设注水的速度为![]() 立方米/每小时,那么有
立方米/每小时,那么有
![]() 得注水的速度
得注水的速度![]() (立方米∕每小时);
(立方米∕每小时);
容器内水的体积![]() 与注水时间
与注水时间![]() 的函数关系式为:
的函数关系式为:![]()
(3)由题意知,上面圆柱的容积与下面圆柱的容积相等,且它的高度为4米,
于是有![]() ,解得
,解得![]()
即上面圆柱的底面半径为![]() 米.
米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把顺序连结四边形各边中点所得的四边形叫中点四边形。
(1)任意四边形的中点四边形是什么形状?为什么?
(2)符合什么条件的四边形,它的中点四边形是菱形?
(3)符合什么条件的四边形,它的中点四边形是矩形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=
 (x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
(x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.(1)求点D的坐标;
(2)点F是OC边上一点,若△FBC和△DEB相似,求点F的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明在数学课外小组活动时遇到这样一个问题:
如果一个不等式(含有不等号的式子)中含有绝对值,并且绝对值符号中含有未知数,我们把这个不等式叫做绝对值不等式.
求绝对值不等式
 的解集(满足不等式的所有解).
的解集(满足不等式的所有解).小明同学的思路如下:
先根据绝对值的定义,求出
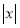 恰好是3时
恰好是3时 的值,并在数轴上表示为点
的值,并在数轴上表示为点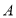 ,
,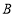 ,如图所示.观察数轴发现,
,如图所示.观察数轴发现,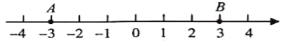
以点
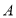 ,
,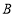 为分界点把数轴分为三部分:
为分界点把数轴分为三部分:点
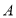 左边的点表示的数的绝对值大于3;
左边的点表示的数的绝对值大于3;点
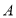 ,
,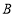 之间的点表示的数的绝对值小于3;
之间的点表示的数的绝对值小于3;点B右边的点表示的数的绝对值大于3.
因此,小明得出结论,绝对值不等式
 的解集为:
的解集为: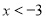 或
或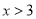 .
.参照小明的思路,解决下列问题:
(1)请你直接写出下列绝对值不等式的解集.
①
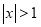 的解集是 ;
的解集是 ;②
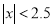 的解集是 .
的解集是 .(2)求绝对值不等式
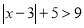 的解集.
的解集.(3)直接写出不等式
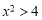 的解集是 .
的解集是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两城相距800千米,一辆客车从甲城开往乙城,车速为
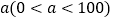 千米
千米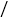 小时,同时一辆出租车从乙城开往甲城,车速为90千米
小时,同时一辆出租车从乙城开往甲城,车速为90千米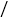 小时,设客车行驶时间为
小时,设客车行驶时间为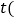 小时
小时
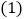 当
当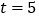 时,客车与乙城的距离为多少千米
时,客车与乙城的距离为多少千米 用含a的代数式表示
用含a的代数式表示
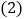 已知
已知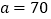 ,丙城在甲、乙两城之间,且与甲城相距260千米
,丙城在甲、乙两城之间,且与甲城相距260千米 求客车与出租车相距100千米时客车的行驶时间;
求客车与出租车相距100千米时客车的行驶时间; 列方程解答
列方程解答
 已知客车和出租车在甲、乙之间的服务站M处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
已知客车和出租车在甲、乙之间的服务站M处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:方案一:继续乘坐出租车到丙城,加油后立刻返回乙城,出租车加油时间忽略不计;
方案二:在M处换乘客车返回乙城.
试通过计算,分析小王选择哪种方案能更快到达乙城?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的顶点A在x轴的正半轴上,顶点D在y轴的正半轴上,点B、点C在第一象限,sin∠OAD=
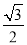 ,线段AD、AB的长分别是方程x2﹣11x+24=0的两根(AD>AB).
,线段AD、AB的长分别是方程x2﹣11x+24=0的两根(AD>AB).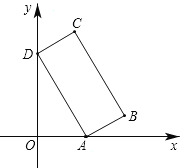
(1)求点B的坐标;
(2)求直线AB的解析式;
(3)在直线AB上是否存在点M,使以点C、点B、点M为顶点的三角形与△OAD相似?若存在,请直接写出点M的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两地相距180km,一列慢车以40km/h的速度从甲地匀速驶往乙地,慢车出发30分钟后,一列快车以60km/h的速度从甲地匀速驶往乙地.两车相继到达终点乙地,再次过程中,两车恰好相距10km的次数是( )
A.1B.2C.3D.4
相关试题

