【题目】在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() .
.
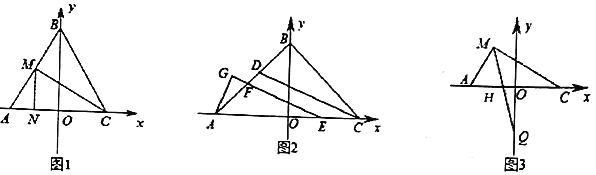
(1)如图1,若![]() ,
,![]() 于点
于点![]() ,
,![]() 轴交
轴交![]() 于点
于点![]() ,则
,则![]() _____.
_____.
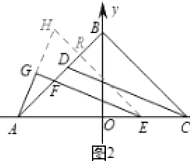
(2)如图2,若![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,过
,过![]() 上一点作
上一点作![]() ,交
,交![]() 于点
于点![]() ,
,![]() 是
是![]() 的高,探究
的高,探究![]() 与
与![]() 的数量关系;
的数量关系;
(3)如图3,在(1)的条件下,![]() 上点
上点![]() 满足
满足![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,求点
,求点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先证明△ABC是等边三角形,然后得到点M是AB的中点,则点N为AO的中点,即可得到A点坐标,求出m的值;
(2)先求出m=n,得到△AOB是等腰直角三角形,然后得到△ABC也是等腰直角三角,则∠ACB=45°,从而得到∠AEG=22.5°,延长![]() 到
到![]() ,使
,使![]() ,连
,连![]() 交
交![]() 于
于![]() ,证明△AEH和△AER是等腰三角形,则得到AR=ER,AH=2AG,然后根据全等得到AH=EF,即可得到
,证明△AEH和△AER是等腰三角形,则得到AR=ER,AH=2AG,然后根据全等得到AH=EF,即可得到![]() ;
;
(3)先证明MQ是∠AMC的角平分线,作![]() 于
于![]() ,
,![]() 于
于![]() ,证明
,证明![]() ≌
≌![]() ,则得到
,则得到![]() ,则
,则![]() ,然后得到OQ=OA,由(1)的结论,即可求出Q点坐标.
,然后得到OQ=OA,由(1)的结论,即可求出Q点坐标.
解:(1)∵![]() ,
,![]() ,
,
∴AO=CO=m,
∴AB=BC=AC,
∴△ABC是等边三角形,
∵![]() ,
,
∴点M是AB的中点,
∵![]() 轴,
轴,
∴点N是AO的中点,
∵点N为![]() ,
,
∴点A为:![]() ,
,
∴![]() ;
;
故答案为:4.
(2)![]()
证明:∵![]() ,
,
∴![]()
∴![]() ,
,
∴![]()
∵![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∵点![]() 与点
与点![]() 关于
关于![]() 轴对称
轴对称
∴![]()
∴![]()
∴![]()
∴![]()
∵![]() 平分
平分![]()
∴![]()
∵![]()
∴![]()
延长![]() 到
到![]() ,使
,使![]() ,连
,连![]() 交
交![]() 于
于![]()
∵![]() 是
是![]() 的高.
的高.
∴![]()
∴![]()
∴![]()
∴![]()
∴![]() ,
,![]()
∴![]()
在![]() 和
和![]() 中,
中,
∵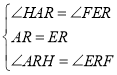
∴![]() ≌
≌![]() (
(![]() )
)
∴![]()
∵![]()
∴![]()
(3)作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
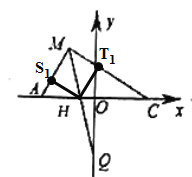
由面积法及![]() ,
,
可得![]()
∴![]() 平分
平分![]()
作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
∴![]()
连接![]() ,则
,则![]()
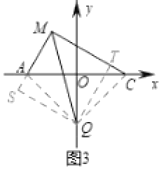
在![]() 和
和![]() 中,
中,
∵![]()
∴![]() ≌
≌![]() (
(![]() )
)
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
由(1)知![]()
∴![]()
∴![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式(x2+mx﹣
 y+3)﹣(3x﹣2y+1﹣nx2).
y+3)﹣(3x﹣2y+1﹣nx2).(1)若多项式的值与字母x的取值无关,求m,n的值;
(2)先化简多项式3(m2﹣mn﹣n2)﹣(3m2+mn+n2),再求它的值;
(3)在(1)的条件下,求(n+m2)+(2n+
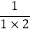 m2)+(3n+
m2)+(3n+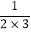 m2)+…+(9n+
m2)+…+(9n+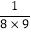 m2).
m2). -
科目: 来源: 题型:
查看答案和解析>>【题目】把正整数1,2,3,4……,排列成如图1所示的一个表,从上到下分别称为第1行、第2行、…,从左到右分别称为第1列、第2列、…….用图2所示的方框在图1中框住16个数,把其中没有被阴影覆盖的四个数分别记为A、B、C、D.设A=x.

(1)在图1中,2018排在第 行第 列;排在第m行第n列的数为 ,其中m≥1,1≤n≤8,且都是正整数;(直接写出答案)
(2)若A+2B+3D=357,求出C所表示的数;
(3)在图(2)中,被阴影覆盖的这些数的和能否为4212?如果能,请求出这些数中最大的数,如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】比较下列各对数的大小:
(1)
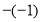 ________
________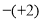 ;(2)
;(2)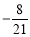 ________
________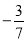 ;(3)
;(3) ________
________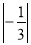 ;(4)
;(4)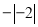 ________
________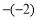
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )

A. 前2分钟,乙的平均速度比甲快
B. 5分钟时两人都跑了500米
C. 甲跑完800米的平均速度为100米/分
D. 甲乙两人8分钟各跑了800米
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个小球由静止开始沿一个斜坡向下滚动,其速度每秒增加2m/s.
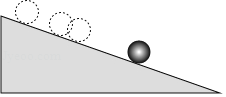
(1)求小球速度v(单位:m/s)关于时间t(单位:s)的函数解析式,它是一次函数吗?
(2)求第3.5s时小球的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若
 是由ABC平移后得到的,且
是由ABC平移后得到的,且 中任意一点
中任意一点 经过平移后的对应点为
经过平移后的对应点为
(1)求点小
 的坐标。
的坐标。(2)求
 的面积。
的面积。
相关试题

