搜索
【题目】如图，在方格纸内将
经过一次平移后得到
，图中标出了点
的对应点
.（小正方形边长为1，的顶点均为小正方形的顶点）
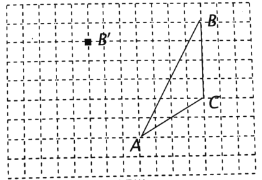
（1）补全；
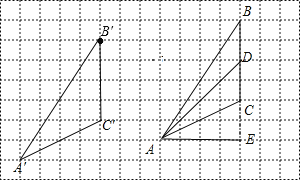
（2）画出中
边上的中线
；
（3）画出中边上的高线
；
（4）的面积为_____.
参考答案：
【答案】（1）如图见解析；（2）如图见解析；（3）如图见解析；（4）
的面积为8.
【解析】
（1）利用点B和B′的位置确定平移的方向与距离，然后利用此平移规律画出A、C的对应点A′、C′即可；
（2）利用网格特点确定BC的中点，从而得到BC边的中线AD；
（3）利用网格特点过A作BC的垂线得到高AE；
（4）根据三角形面积公式计算．
解：（1）如图，△A′B′C′为所作；
（2）如图，AD为所作；
（3）AE为所作；
（4）△A′B′C′的面积=
×4×4=8，
故答案为8．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,四边形ABCD中,∠ABC、∠ADC的平分线分別交CD、AB上点E、F.
(1)若∠ABC=∠ADC,求征:∠ADF=∠ABE;
(2)如图，若∠A与∠C互朴，试探究∠ADF与∠ABE之同的数量夫系，并说明理由;
(3)如图,在(2)的条件下，当DA⊥AB时，试探究BE与DF的位置关系，并说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（知识回顾）
七年级学习代数式求值时，遇到这样一类题“代数式
的值与
的取值无关，求
的值”，通常的解题方法是:把、
看作字母，看作系数合并同类项，因为代数式的值与的取值无关，所以含项的系数为0,即原式=
,所以
,则
.（理解应用）
(1)若关于
的多项式
的值与的取值无关，求m值;(2)已知
，
,且3A+6B的值与无关，求的值;（能力提升）
(3)7张如图1的小长方形，长为
,宽为
,按照图2方式不重叠地放在大长方形ABCD内，大长方形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为
,左下角的面积为
,当AB的长变化时，
的值始终保持不变，求与的等量关系.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点（点A在点B的左侧），其对称轴l与x轴交于点C，它的顶点为点D．
（1）写出点D的坐标 ．
（2）点P在对称轴l上，位于点C上方，且CP=2CD，以P为顶点的二次函数y2=ax2+bx+c（a≠0）的图象过点A．
①试说明二次函数y2=ax2+bx+c（a≠0）的图象过点B；
②点R在二次函数y1=（x﹣2）（x﹣4）的图象上，到x轴的距离为d，当点R的坐标为 时，二次函数y2=ax2+bx+c（a≠0）的图象上有且只有三个点到x轴的距离等于2d；
③如图2，已知0＜m＜2，过点M（0，m）作x轴的平行线，分别交二次函数y1=（x﹣2）（x﹣4）y2=ax2+bx+c（a≠0）的图象于点E、F、G、H（点E、G在对称轴l左侧），过点H作x轴的垂线，垂足为点N，交二次函数y1=（x﹣2）（x﹣4）的图象于点Q，若△GHN∽△EHQ，求实数m的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一辆汽车往返于甲、乙两地之间，如果汽车以50千米/时的平均速度从甲地出发，则6小时可到达乙地．
（1）写出时间t（时）关于速度v（千米/时）的函数关系式，并画出函数图象．
（2）若这辆汽车需在5小时内从甲地到乙地，则此时汽车的平均速度至少应是多少？
-
科目： 来源： 题型：
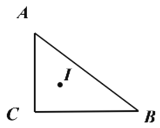
查看答案和解析>>【题目】在Rt△ABC中，∠C=90°，AB=10，BC=8，AC=6.点I为△ABC三条角平分线的交点，则点I到边AB的距离为__________
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，点A（2,0）B（0,4）.以AB为斜边作等腰直角△ABC，则点C坐标为__________
相关试题
