Question

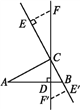
【题目】(2017·河北迁安一模)如图,在Rt△ABC中,直角边AC=7 cm,BC=3 cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2 cm/s的速度移动,过点E作BC的垂线交直线CD于点F.

(1)试说明:∠A=∠BCD;

(2)点E运动多长时间,CF=AB?并说明理由.

Answer 1

【答案】（1）理由见解析；（2）当点E在射线BC上移动5 s或2 s时,CF=AB.

【解析】试题分析：(1)、根据同角的余角相等得出答案；(2)、首先根据题意画出两个不同的图形，然后根据三角形全等得出线段的长度，从而得出运动的时间．

试题解析：(1)因为∠A+∠ACD=90°,∠BCD+∠ACD=90°, 所以∠A=∠BCD.

(2)如图,当点E在射线BC上移动时,若点E移动5 s,则BE=2×5=10(cm),

所以CE=BE-BC=10-3=7(cm). 所以CE=AC.

在△CFE与△ABC中, 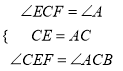所以△CFE≌△ABC, 所以CF=AB.

当点E在射线CB上移动时,若点E移动2 s,则BE'=2×2=4(cm),

所以CE'=BE'+BC=4+3=7(cm), 所以CE'=AC.

在△CF'E'与△ABC中, 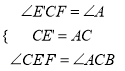所以△CF'E'≌△ABC. 所以CF'=AB.

总之,当点E在射线BC上移动5 s或2 s时,CF=AB.