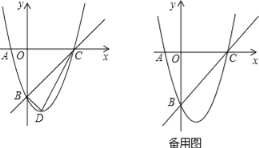
【题目】已知,m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),如图所示.
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为C,抛物线的顶点为D,试求出点C,D的坐标,并判断△BCD的形状.
参考答案:
【答案】(1)y=x2-2x-3;(2)C(3,0),D(1,-4),△BCD是直角三角形.
【解析】
(1)先解一元二次方程,然后用待定系数法求出抛物线解析式;
(2)先解方程求出抛物线与x轴的交点,再判断出△BOC和△BED都是等腰直角三角形,从而得到结论.
(1)∵x2+4x+3=0,∴x1=﹣1,x2=﹣3.
∵m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,∴m=﹣1,n=﹣3.
∵抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),∴![]() ,∴
,∴![]() ,∴抛物线解析式为y=x2﹣2x﹣3;
,∴抛物线解析式为y=x2﹣2x﹣3;
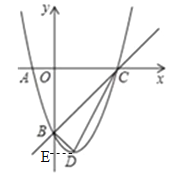
(2)令y=0,则x2﹣2x﹣3=0,∴x1=﹣1,x2=3,∴C(3,0).
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴顶点坐标D(1,﹣4).
过点D作DE⊥y轴.
∵OB=OC=3,∴BE=DE=1,∴△BOC和△BED都是等腰直角三角形,∴∠OBC=∠DBE=45°,∴∠CBD=90°,∴△BCD是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知RtΔABC,∠C=90°,D为BC的中点.以AC为直径的圆O交AB于点E.
(1)求证:DE是圆O的切线.
(2)若AE:EB=1:2,BC=6,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】随若移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A .和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如下图表(部分信息未给出):

根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中
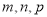 的值,并补全条形统计图;
的值,并补全条形统计图;(3)若该中学约有
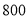 名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调査结果,就中学生如何合理使用手机给出你的一条建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°,∠C=45°

(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:
 ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是关于
是关于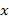 的方程
的方程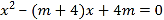 的一个实数根,并且这个方程的两个实数根恰好是等腰三角形
的一个实数根,并且这个方程的两个实数根恰好是等腰三角形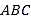 的两条边长,则
的两条边长,则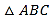 的周长为( )
的周长为( )A. 6 B. 8 C. 10 D. 8或10
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学准备购买笔和本子送给农村希望小学的同学,在市场上了解到某种本子的单价比某种笔的单价少4元,且用30元买这种本子的数量与用50元买这种笔的数量相同.
(1)求这种笔和本子的单价;
(2)该同学打算用自己的100元压岁钱购买这种笔和本子,计划100元刚好用完,并且笔和本子都买,请列出所有购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
相关试题

