【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P,根据下列条件,求∠BPC的度数.
(1)若∠ABC=50°,∠ACB=60°,则∠BPC= ;
(2)若∠ABC+∠ACB=120°,则∠BPC= ;
(3)若∠A=80°,则∠BPC= ;
(4)从以上的计算中,你能发现已知∠A,求∠BPC的公式是:∠BPC= (提示:用∠A表示).

参考答案:
【答案】(1)125°;(2)120°;(3)130°;(4)90°+![]() ∠A.
∠A.
【解析】
(1)由∠ABC=50°,∠ACB=60°,∠2+∠4=25°+30°=55°,在△BCP中,由三角形内角和为180°可得答案;
(2)同理,由ABC+∠ACB=120°,∠ABC和∠ACB的平分线相交于点P,可得∠2+∠4=![]() ×120°=60°,在△BCP中,由三角形内角和为180°可得答案;
×120°=60°,在△BCP中,由三角形内角和为180°可得答案;
(3) A=80°,可得ABC+∠ACB=100°,∠2+∠4=![]() ×100°=50°,可得∠BPC的度数;
×100°=50°,可得∠BPC的度数;
(4)ABC+∠ACB=180°﹣∠A,∠ABC和∠ACB的平分线相交于点P,可得∠2+∠4=![]() ×(180°﹣∠A),在△BCP中,∠P=180°﹣
×(180°﹣∠A),在△BCP中,∠P=180°﹣![]() ×(180°﹣∠A)=90°+
×(180°﹣∠A)=90°+![]() ∠A
∠A
解:(1)∵∠ABC=50°,∠ACB=60°,∠ABC和∠ACB的平分线相交于点P,
∴∠2+∠4=25°+30°=55°,
∴△BCP中,∠P=180°﹣55°=125°,
故答案为:125°;
(2)∵∠ABC+∠ACB=120°,∠ABC和∠ACB的平分线相交于点P,
∴∠2+∠4=![]() ×120°=60°,
×120°=60°,
∴△BCP中,∠P=180°﹣60°=120°,
故答案为:120°;
(3)∵∠A=80°,
∴∠ABC+∠ACB=100°,
∠ABC和∠ACB的平分线相交于点P,
∴∠2+∠4=![]() ×100°=50°,
×100°=50°,
∴△BCP中,∠P=180°﹣50°=130°,
故答案为:130°;
(4))∵∠ABC+∠ACB=180°﹣∠A,∠ABC和∠ACB的平分线相交于点P,
∴∠2+∠4=![]() ×(180°﹣∠A),
×(180°﹣∠A),
∴△BCP中,∠P=180°﹣![]() ×(180°﹣∠A)=90°+
×(180°﹣∠A)=90°+![]() ∠A.
∠A.
故答案为:90°+![]() ∠A.
∠A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min 才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m,图中 的折线表示小亮在整个行走过程中y与x的函数关系.
(1)小亮行走的总路程是___________m,他途中休息了_____________min;
(2)①当50<x<80时,求y与x的函数关系式;②当小颖到达缆车终点时,小亮离缆车终点的路程是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
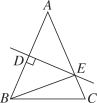
(1)如图1,△ABC中,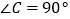 ,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为;
,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为;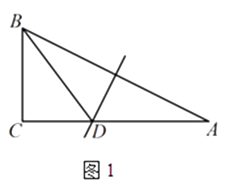
(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中求作△EDF(要求:尺规作图,不写作法,保留作图痕迹);
②在图3中补全图形,求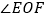 的度数;
的度数;
③若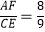 ,则
,则 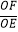 的值为 .
的值为 . 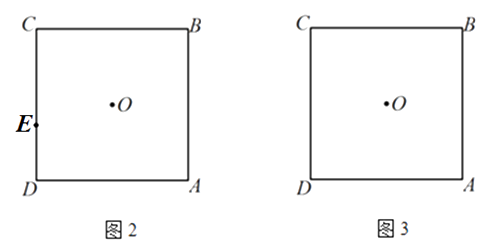
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,交AB于点D.
(1)若∠A=40°,求∠CBE的度数;
(2)若△BCE的周长为8cm,AB=5cm,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在关系式
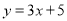 中有下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图像表示;⑤y与x的关系还可以用列表法和图像法表示,其中说法正确的是( ).
中有下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图像表示;⑤y与x的关系还可以用列表法和图像法表示,其中说法正确的是( ).A.①②⑤B.①②④C.①③⑤D.①④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD四个顶点都在⊙O上,点P是在弧AB上的一点,则∠CPD的度数是( )
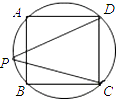
A.35°
B.40°
C.45°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)(-78) +(+5)+(+78) (2)(+23)+(-17)+(+6)+(-22)
(3)[45-(
 -
-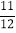 +
+ )×36]÷5 (4)99
)×36]÷5 (4)99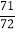 ×(-36)
×(-36)
相关试题

