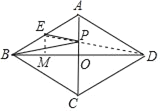
【题目】如图，在菱形ABCD中，AC与BD相交于点O，AB＝4，BD＝4，E为AB的中点，点P为线段AC上的动点，则EP+BP的最小值为（　　）

A. 4B. 2C. 2D. 8

参考答案：

【答案】C

【解析】

连结DE交AC于点P，连结BP，根据菱形的性质推出AO是BD的垂直平分线，推出PE+PB=PE+PD=DE且值最小，根据勾股定理求出DE的长即可．

如图，设AC，BD相交于O，

∵四边形ABCD是菱形，

∴AC⊥BD，AO＝AC，BO＝BD＝2，

∵AB＝4，

∴AO＝2，

连结DE交AC于点P，连结BP，作EM⊥BD于点M，

∵四边形ABCD是菱形，

∴AC⊥BD，且DO＝BO，即AO是BD的垂直平分线，

∴PD＝PB，

∴PE+PB＝PE+PD＝DE且值最小，

∵E是AB的中点，EM⊥BD，

∴EM＝AO＝1，BM＝BO＝，

∴DM＝DO+OM＝BO＝3，

∴DE＝，

故选C．

关闭