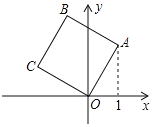
【题目】如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,2),则点C的坐标为_____.
参考答案:
【答案】(﹣2,1).
【解析】
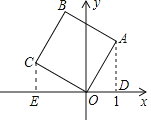
过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,根据正方形的性质和同角的余角相等证出:OA=OC,∠OAD=∠COE,然后利用AAS即可证出△AOD≌△OCE,从而得出OE=AD=2,CE=OD=1,再结合C点所在象限即可求出C点坐标.
解:过点A作AD⊥x轴于D,过点C作CE⊥x轴于E, 如图所示
∵四边形OABC是正方形,
∴OA=OC,∠AOC=90°,
∴∠COE+∠AOD=90°,
又∵∠OAD+∠AOD=90°,
∴∠OAD=∠COE,
在△AOD和△OCE中,
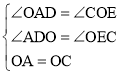 ,
,
∴△AOD≌△OCE(AAS),
∴OE=AD=2,CE=OD=1,
∵点C在第二象限,
∴点C的坐标为(﹣2,1).
故答案为(﹣2,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图⑴,在△ABC中,∠ABC 、∠ACB的平分线相交于点O,试说明∠BOC=90°+
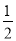 ∠A;
∠A;(2)如图⑵,在△ABC中,BD、CD分别是∠ABC 、∠ACB的外角平分线,试说明∠D=90°-
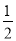 ∠A;
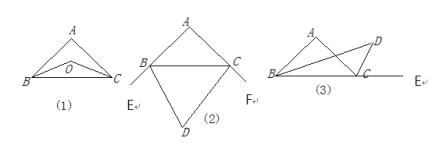
∠A;(3)如图⑶,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D,试说明∠A=2∠D。
-
科目: 来源: 题型:
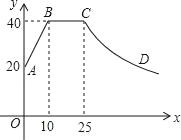
查看答案和解析>>【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB,BC分别为线段,CD为双曲线的一部分):
(1)分别求出线段AB和曲线CD的函数关系式;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
-
科目: 来源: 题型:
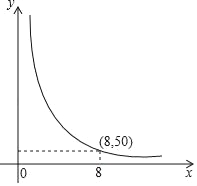
查看答案和解析>>【题目】码头工人每天往一艘轮船上装载货物,平均每天装载速度y(吨/元)与装完货物所需时间x(天)之间是反比例函数关系,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)由于紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸货多少吨?
(3)若码头原有工人10名,且每名工人每天的装卸量相同,装载完毕恰好用了8天时间,在(2)的条件下,至少需要增加多少名工人才能完成任务?
-
科目: 来源: 题型:
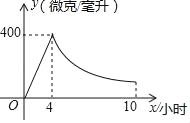
查看答案和解析>>【题目】驾驶员血液中每毫升的酒精含量大于或等于200微克即为酒驾,某研究所经实验测得:成人饮用某品牌38度白酒后血液中酒精浓度y(微克/毫升)与饮酒时间x(小时)之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中酒精浓度上升和下降阶段y与x之间的函数表达式.
(2)问血液中酒精浓度不低于200微克/毫升的持续时间是多少小时?
-
科目: 来源: 题型:
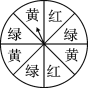
查看答案和解析>>【题目】如图是一个转盘,转盘分成8个相同的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).求下列事件的概率:
(1)指针指向红色;(2)指针指向黄色或绿色.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,D,E是半圆上任意两点,连接AD,DE,AE与BD相交于点C,要使△ADC与△BDA相似,可以添加一个条件.下列添加的条件中错误的是( )

A. ∠ACD=∠DAB B. AD=DE C. AD·AB=CD·BD D. AD2=BD·CD
相关试题

