【题目】如图,直线l过正方形ABCD的顶点B,点A,C到直线l的距离AE,CF分别为5和3,则正方形ABCD的面积是________.

参考答案:
【答案】34
【解析】
由ABCD为正方形得到AB=BC,∠ABC为直角,再由AE与CF都垂直于EF,利用同角的余角相等得到一对角相等,再由一对直角相等,;利用AAS得出三角形ABE与三角形BCF全等,由全等三角形对应边相等得到AE=BF,EB=CF,在直角三角形ABE中,利用勾股定理求出AB的长,即可确定出正方形的面积.
∵ABCD为正方形,
∴AB=BC,∠ABC=90°,
∵AE⊥EF,CF⊥EF,
∴∠AEB=∠BFC=90°,
∴∠BAE+∠ABE=90°,∠ABE+∠CBF=90°,
∴∠BAE=∠CBF,
在△ABE和△BCF中,
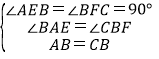 ,
,
∴△ABE≌△BCF(AAS),
∴AE=BF=5,CF=EB=3,
根据勾股定理得:AB=![]() =
=![]() ,
,
则正方形ABCD面积为34.
故答案为:34
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)13+(﹣15)﹣(﹣23);
(2)23×(﹣5)﹣(﹣3)÷
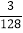 ;
;(3)﹣14﹣
 ×[2﹣(﹣3)2];
×[2﹣(﹣3)2];(4)﹣(2y﹣5)+(4+3y)
-
科目: 来源: 题型:
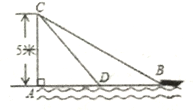
查看答案和解析>>【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数y=﹣
 (x﹣2)2﹣3,下列说法错误的是( )
(x﹣2)2﹣3,下列说法错误的是( )
A.图象的开口向下
B.当x=2时,y有最大值﹣3
C.图象的顶点坐标为(2,﹣3)
D.图象与y轴的交点坐标为(0,﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )

A. =
= 
B. =
= 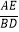
C. =
= 
D. =
= 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为绿化校园,安排七年级三个班植树,其中,一班植树x棵,二班植树的棵数是一班的2倍少20棵,三班植树的棵数是二班的一半多15棵.
(1)三个班共植树多少棵?(用含x的式子表示)
(2)当x=30时,三个班中哪个班植树最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OM,ON分别是∠BOC和∠AOC的角平分线,∠AOB=86°,(1)∠MON=______(度);(2)当OC在∠AOB内绕点O转动时,∠MON的值______改变(填“会”或“不会”).

相关试题

