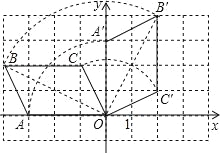
【题目】如图,在平面直角坐标系中,四边形OABC四个顶点的坐标分别为O(0,0),A(﹣3,0),B(﹣4,2),C(﹣1,2).将四边形OABC绕点O顺时针旋转90°后,点A、B、C分别落在点A′、B′、C′处.
(1)请你在所给的直角坐标系中画出旋转后的四边形OA′B′C′;
(2)点C旋转到点C′所经过的弧的半径是 ,点C经过的路线长是 .

参考答案:
【答案】![]() π.
π.
【解析】
试题分析:(1)根据网格结构找出点A、B、C的对应点A′、B′、C′的位置,然后顺次连接即可;
(2)先利用勾股定理求出OC的长度,再根据弧长的计算公式列式进行计算即可得解.
试题解析:(1)如图所示,四边形OA′B′C′即为所求作的图形;
(2)根据勾股定理,OC=![]() =
=![]() ,
,
C经过的路线长=![]() =
=![]() π.
π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣2x)2的结果是( )
A.2x2B.﹣2x2C.4x2D.﹣4x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,AF=AB,已知△ABE≌△ADF.
(1)在图中,可以通过平移、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置;
(2)线段BE与DF有什么关系?证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校初三400名学生的体重情况,从中抽取50名学生的体重进行分析.在这项调查中,下列说法正确的是( )
A.400名学生中每位学生是个体
B.400名学生是总体
C.被抽取的50名学生是总体的一个样本
D.样本的容量是50
-
科目: 来源: 题型:
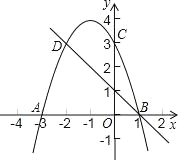
查看答案和解析>>【题目】如图,二次函数y1=ax2+bx+3的图象与x轴相交于点A(﹣3,0)、B(1,0),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数y2=mx+n的图象经过B、D两点.
(1)求二次函数的解析式及点D的坐标;
(2)根据图象写出y2>y1时,x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式一定成立的是( )
A.2a+3b=5ab
B.(a3)2=a5
C.a2a3=a5
D.(a+b)2=a2+b2
相关试题

