【题目】题目:如图,直线a,b被直线所截,若∠1+∠7=180°,则a∥b.在下面说理过程中的括号里填写说理依据.
方法一:∵∠1+∠7=180°(已知)
而∠1+∠3=180°(平角定义)
∴∠7=∠3()
∴a∥b()
方法二::∵∠1+∠7=180°(已知)
∠1+∠3=180°(平角定义)
∴∠7=∠3()
又∠7=∠6()
∴∠3=∠6()
∴a∥b()
方法三::∵∠1+∠7=180°(已知)
而∠1=∠4,∠7=∠6()
∠4+∠6=180°(平角定义)
∴a∥b()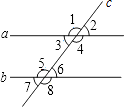
参考答案:
【答案】同角的补角相等;同位角相等,两直线平行;同角的补角相等;对顶角相等;等量代换;内错角相等,两直线平行;顶角相等;同旁内角互补,两直线平行
【解析】解:方法一:∵∠1+∠7=180°(已知)
而∠1+∠3=180°(平角定义)
∴∠7=∠3(同角的补角相等)
∴a∥b(同位角相等,两直线平行)
方法二:∵∠1+∠7=180°(已知)
∠1+∠3=180°(平角定义)
∴∠7=∠3(同角的补角相等)
又∠7=∠6(对顶角相等)
∴∠3=∠6(等量代换)
∴a∥b(内错角相等,两直线平行)
方法三:∵∠1+∠7=180°(已知)
而∠1=∠4,∠7=∠6(对顶角相等)
∠4+∠6=180°(平角定义)
∴a∥b(同旁内角互补,两直线平行).
故答案是:方法一:同角的补角相等;同位角相等,两直线平行;
方法二:同角的补角相等;对顶角相等;等量代换;内错角相等,两直线平行;
方法三:对顶角相等;同旁内角互补,两直线平行.
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE,
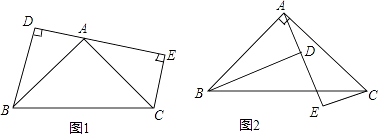
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,我们能得到什么结论?并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣1)2017+(﹣
 )﹣3﹣(2017)0的结果是( )
)﹣3﹣(2017)0的结果是( )
A.﹣10
B.﹣8
C.8
D.﹣9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AD平分∠BAC,AB=AC,连结BD、CD并延长分别交AC、AB于F、E点,则此图中全等三角形的对数为( )
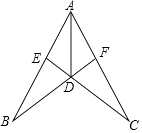
A.2对
B.3对
C.4对
D.5对 -
科目: 来源: 题型:
查看答案和解析>>【题目】小敏尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②); 再沿过D点的直线折叠, 使得 C点落在DA边上的点N处, E点落在AE边上的点M处,折痕为 DG(如图).如果第二次折叠后,M点正好在∠NDG的平分线上,那么矩形ABCD的长与宽的比值为( )
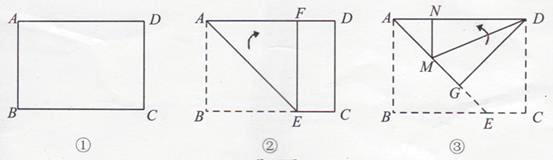
A.2
B.3
C.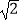
D.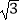
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b的图象与反比例函数
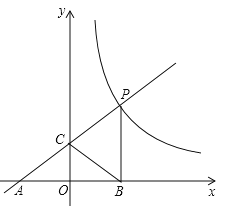
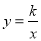 (x>0)的图象交于点P(m,4),与x轴交于点A(﹣3,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(m,4),与x轴交于点A(﹣3,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.(1)求反比例函数与一次函数的解析式;
(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
-
科目: 来源: 题型:
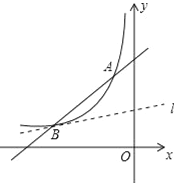
查看答案和解析>>【题目】如图,一次函数y=x+b的图象与反比例函数
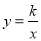 (k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).
(k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).(1)求反比例函数的表达式和a、b的值;
(2)若A、O两点关于直线l对称,请连接AO,并求出直线l与线段AO的交点坐标.
相关试题

