【题目】小聪和小敏在研究绝对值的问题时,遇到了这样一道题:
(1)当式子|x﹣1|+|x+5|取最小值时,x应满足的条件是 , 此时的最小值是 . 小聪说:利用数轴求线段的长可以解决这个问题.如图,点A,B对应的数分别为﹣5,1,则线段AB的长为6,我发现也可通过|1﹣(﹣5)|或|﹣5﹣1|来求线段AB的长,即数轴上两点间的线段的长等于它们所对应的两数差的绝对值.![]()
小敏说:我明白了,若点C在数轴上对应的数为x,线段AC的长就可表示为|x﹣(﹣5)|,那么|x﹣1|表示的是线段的长.
小聪说:对,求式子|x﹣1|+|x+5|的最小值就转化为数轴上求线段AC+BC长的最小值,而点C在线段AB上时AC+BC=AB最小,最小值为6.
小敏说:点C在线段AB上,即x取﹣5,1之间的有理数(包括﹣5,1),因此相应x的取值范围可表示为﹣5≤x≤1时,最小值为6.
请你根据他们的方法解决下面的问题:
(2)小敏说的|x﹣1|表示的是线段的长;
(3)当式子|x﹣3|+|x+2|取最小值时,x应满足的条件是;
(4)当式子|x﹣2|+|x+3|+|x+4|取最小值时,x应满足的条件是;
(5)当式子|x﹣a|+|x﹣b|+|x﹣c|+|x﹣d|(a<b<c<d)取最小值时,x应满足的条件是 , 此时的最小值是 .
参考答案:
【答案】
(1)﹣5≤x≤1;6;BC
(2)BC
(3)﹣2≤x≤3
(4)x=﹣3
(5)b≤x≤c;c﹣b+d﹣a
【解析】解:(2)由题意可知:|x﹣1|=BC;(3)由题意可知:﹣2≤x≤3;(4)|x﹣2|+|x+3|+|x+4|表示数x分别与﹣4、﹣3、2的距离之和,由题意可知:当﹣3≤x≤2时,|x+3|+|x﹣2|可取得最小值,∴当x=﹣3时,|x﹣2|+|x+3|+|x+4|可取得最小值,(5)由题意可知:|x﹣a|+|x﹣b|+|x﹣c|+|x﹣d|表示数x分别与a、b、c、d的距离之和,∴b≤x≤c时,x﹣a|+|x﹣b|+|x﹣c|+|x﹣d|的最小值为:c﹣b+d﹣a.所以答案是:(1)﹣5≤x≤1,6,BC(2)BC(3)﹣2≤x≤3(4)x=﹣3(5)b≤x≤c,c﹣b+d﹣a.根据绝对值的性质以及题意即可求出答案.
【考点精析】根据题目的已知条件,利用数轴和绝对值的相关知识可以得到问题的答案,需要掌握数轴是规定了原点、正方向、单位长度的一条直线;正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离.
-
科目: 来源: 题型:
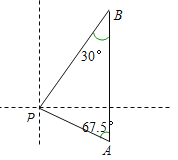
查看答案和解析>>【题目】马航MH370 客机“失联”,我国“海巡01号”前往搜寻。如图某天上午9时,“海巡01号” 轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】能断定A,B,C三点共线的是( )
A. AB=6,AC=2,BC=5B. AB=6,AC=2,BC=4
C. AB=6,AC=3,BC=4D. AB=6,AC=5,BC=4
-
科目: 来源: 题型:
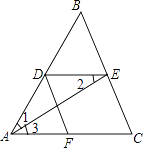
查看答案和解析>>【题目】在△ABC中,AE平分∠BAC交BC于E,DE∥AC交AB于D,过D作DF∥BC交AC于F,若AD=3,求FC.
-
科目: 来源: 题型:
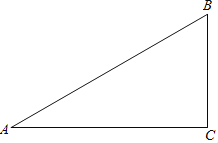
查看答案和解析>>【题目】已知:如图,在△ABC中,∠A=30°,∠B=60°。
(1)作∠B的平分线BD,交AC于点D;作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作
法和证明);
(2)连接DE,求证:△ADE≌△BDE。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣15﹣(﹣8)+(﹣11)﹣12
(2)﹣23+[(﹣4)2﹣(1﹣32)×3]. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于抛物线y=-x2+2的说法正确的是( )
A. 抛物线开口向上B. 顶点坐标为(-1,2)
C. 在对称轴的右侧,y随x的增大而增大D. 在对称轴的左侧,y随x的增大而增大
相关试题

