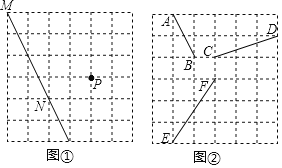
【题目】如图,在6×6的正方形网格中,每个小正方形的边长为1,点A、B、C、D、E、F、M、N、P均为格点(格点是指每个小正方形的顶点).
(1)利用图①中的网格,过P点画直线MN的平行线和垂线.
(2)把图②网格中的三条线段AB、CD、EF通过平移使之首尾顺次相接组成一个三角形(在图②中画出三角形).
(3)第(2)小题中线段AB、CD、EF首尾顺次相接组成一个三角形的面积是______.
参考答案:
【答案】(1)见解析;(2)见解析;(3)3.5
【解析】
(1)根据网格结构的特点,利用直线与网格的夹角的关系找出与AB平行的格点以及垂直的格点作出即可;
(2)根据网格结构的特点,过点E找出与AB、CD位置相同的线段,过点F找出与AB、CD位置相同的线段,作出即可;
(3)依据割补法进行计算,即可得到三角形的面积.
(1)如图①,PQ∥MN,PN⊥MN;
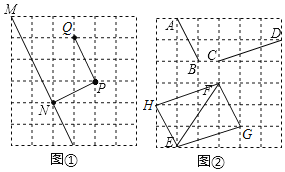
(2)如图②,△EFG或△EFH即为所求;
(3)三角形的面积为:3×3-![]() ×1×2-
×1×2-![]() ×1×3-
×1×3-![]() ×2×3=9-1-1.5-3=3.5,
×2×3=9-1-1.5-3=3.5,
故答案为:3.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好地治理水质,保护环境,某污水处理公司决定购买10台污水处理设备,现有A、B两种设备可供选择,月处理污水分别为240m3/月、200m3/月.经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少8万元.
(1)A、B两种型号的设备每台的价格是多少?
(2)若污水处理公司购买设备的预算资金不超过125万元,你认为该公司有哪几种购买方案?
(3)若每月需处理的污水约2040m3,在不突破(2)中资金预算的前提下,为了节约资金,又要保证治污效果,请你为污水处理公司设计一种最省钱的方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张.

(1)请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果(卡片用A,B,C,D表示);
(2)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图8中图①,两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向
右平移到△A′B′D′的位置得到图②,则阴影部分的周长为_________

-
科目: 来源: 题型:
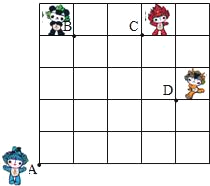
查看答案和解析>>【题目】如图,奥运福娃在5×5的方格(每个格边长尾1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:
B→A(﹣4,﹣1).请根据图中所给信息解决下列问题:
(1)A→C(______),_____);
B→C(______),_____);C→_____(﹣4,﹣3);
(2)如果贝贝的行走路线为A→B→C→D,请计算贝贝走过的路程;
(3)如果贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),
(+2,﹣1),(﹣2,+3),(﹣1,﹣1),请在图中标出妮妮的位置E点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图一,现有足够多的边长为
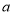 的小正方形纸片(
的小正方形纸片(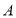 类)、长为
类)、长为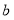 宽为
宽为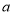 的长方形纸片(
的长方形纸片(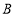 类)以及边长为
类)以及边长为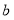 的大正方形纸片(
的大正方形纸片(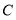 类).
类).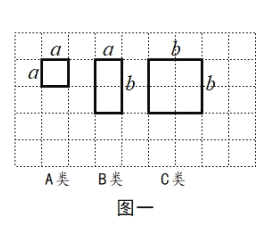
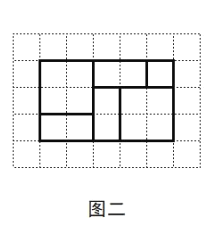
如图二,小明利用上述三种纸片各若干张,拼出了一个长为
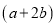 ,宽为
,宽为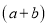 的长方形,并用这个长方形解释了等式
的长方形,并用这个长方形解释了等式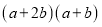
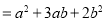 是成立的.
是成立的.(1)若取图一中的纸片若干张(三种都要取到)拼成一个长方形(所取纸片用完无剩余),使它的长和宽分别为
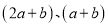 ,请你通过计算说明需要
,请你通过计算说明需要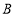 类卡片多少张;
类卡片多少张;(2)若取
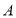 类纸片
类纸片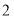 张,
张,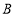 类纸片
类纸片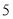 张,
张,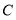 类纸片
类纸片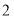 张,能拼成一个长方形吗(所取纸片用完无剩余)?请你在图三中画出示意图并在下面直接写出能用该长方形来解释成立的等式;
张,能拼成一个长方形吗(所取纸片用完无剩余)?请你在图三中画出示意图并在下面直接写出能用该长方形来解释成立的等式;

(3)如图四,大正方形的边长为
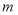 ,小正方形的边长为
,小正方形的边长为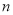 ,用四个完全相同的长方形的长和宽为别为
,用四个完全相同的长方形的长和宽为别为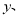
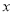 .请你通过观察或计算,判断下列
.请你通过观察或计算,判断下列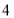 个式子是否成立,将其中成立的式子的都填写在横线上: (直接填写序号).
个式子是否成立,将其中成立的式子的都填写在横线上: (直接填写序号).①
 ;
;②
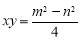 ;
;③
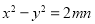 ;
;④
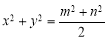 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,反比例函数y=
 (x>0)的图象上有一点A(a,3),过点A作AB⊥x轴于点B,将点B沿x轴正方向平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数于点D,CD=
(x>0)的图象上有一点A(a,3),过点A作AB⊥x轴于点B,将点B沿x轴正方向平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数于点D,CD=  ,直线AD与x轴交于点M,与y轴交于点N.
,直线AD与x轴交于点M,与y轴交于点N.
(1)用含a的式子表示点D的横坐标为:;
(2)求a的值和直线AD的函数表达式;
(3)请判断线段AN与MD的数量关系,并说明理由;
(4)若一次函数y1=k1x+b1经过点(10,9),与双曲线y= (x>0)交于点P,且该一次函数y1的值随x的增大而增大,请确定P点横坐标n的取值范围(不必写出过程)
(x>0)交于点P,且该一次函数y1的值随x的增大而增大,请确定P点横坐标n的取值范围(不必写出过程)
相关试题

