【题目】如图,在正方形ABCD中,AB=6,E是BC边的中点,F是CD边上的一点,且DF=2,若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为 .

参考答案:
【答案】![]() .
.
【解析】分析:作点F关于AD的对称点G,过G作GN⊥AE与N,交AD于M,则GN的长度等于MN+MF的最小值,根据对称的性质得到∠DMF=∠GMD,根据余角的性质得到∠FMD=∠BAE=∠AMN,根据相似三角形的性质和勾股定理即可得到结论.
详解:作点F关于AD的对称点G,过G作GN⊥AE与N,交AD于M ,
则GN的长度等于MN+MF的最小值,
∵△DGM≌△DFM, ∴∠DMF=∠GMD , ∵∠GMD=∠AMN ,
∵∠AMN+∠MAN=∠MAN+∠BAE=90 ,∴∠FMD=∠BAE=∠AMN ,
∴△ABE∽△DMF∽△AMN , ∴![]() , ∵AB=6, ∴BE=3,
, ∵AB=6, ∴BE=3,
∵DF=2, ∴DM=4, ∴AM=2, ∵![]() , ∴MN=
, ∴MN=![]() ,
,
∵GM=![]() ,
,
∴GN=GM+MN=MN+MF=![]() , ∴MN+MF 的最小值为
, ∴MN+MF 的最小值为![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的有( )个
①互为相反数的数的立方根也互为相反数;
② 不是整式;
不是整式;
③算术平方根等于它本身的数只有零;
④实数和数轴上的点一一对应;
⑤任何两数相加,和不小于任何一个加数.A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点是B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①abc>0;②方程ax2+bx+c=3有两个相等的实数根;③抛物线与x轴的另一个交点是(﹣1,0);④当1<x<4时,有y2>y1;⑤x(ax+b)≤a+b,其中正确的结论是 .(只填写序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,等腰直角三角形
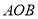 的直角顶点
的直角顶点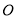 在坐标原点,点
在坐标原点,点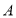 的坐标为
的坐标为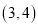 ,求点
,求点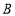 的坐标.
的坐标.(2)依据(1)的解题经验,请解决下面问题:
如图2,点
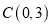 ,
,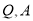 两点均在
两点均在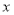 轴上,且
轴上,且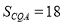 ,分别以
,分别以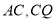 为腰在第一、第二象限作等腰
为腰在第一、第二象限作等腰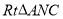 ,
,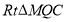 连接
连接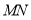 ,与
,与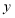 轴交于点
轴交于点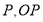 的长度是否发生改变?若不变,求
的长度是否发生改变?若不变,求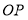 的值;若变化,求
的值;若变化,求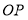 的取值范围.
的取值范围.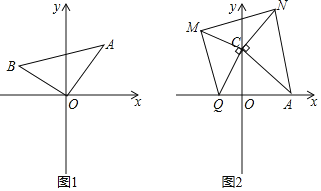
-
科目: 来源: 题型:
查看答案和解析>>【题目】庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言):1=


图2也是一种无限分割:在△ABC中,∠C=90°,∠B=30°,过点C作CC1⊥AB于点C1,再过点C1作C1C2⊥BC于点C2,又过点C2作C2C3⊥AB于点C3,如此无限继续下去,则可将利△ABC分割成△ACC1、△CC1C2、△C1C2C3、△C2C3C4、…、△Cn﹣2Cn﹣1Cn、….假设AC=2,这些三角形的面积和可以得到一个等式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形
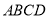 中,
中, ,则添加下列条件,不能使四边形
,则添加下列条件,不能使四边形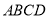 成为平行四边形的是( )
成为平行四边形的是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
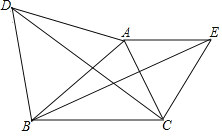
查看答案和解析>>【题目】如图,已知△ABC ,分别以AB 、AC 为边在△ABC 的外部作等边三角形ABD和等边三角形ACE联结DC 、BE 试说明DCBE的理由.
相关试题

