【题目】.如图 1,AB∥CD,直线 EF 交 AB 于点 E,交 CD 于点 F,点 G 在 CD 上,点 P在直线 EF 左侧,且在直线 AB 和 CD 之间,连接 PE,PG.
(1) 求证: ∠EPG=∠AEP+∠PGC;
(2) 连接 EG,若 EG 平分∠PEF,∠AEP+ ∠ PGE=110°,∠PGC=![]() ∠EFC,求∠AEP 的度数.
∠EFC,求∠AEP 的度数.
(3) 如图 2,若 EF 平分∠PEB,∠PGC 的平分线所在的直线与 EF 相交于点 H,则∠EPG 与∠EHG之间的数量关系为 .
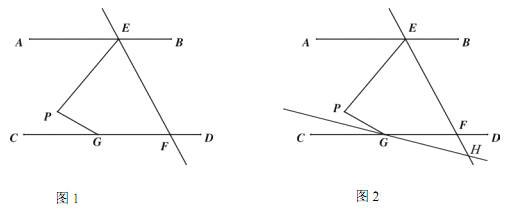
参考答案:
【答案】(1)见解析;(2)40°;(3) ∠EPG=1800-2∠EHG .
【解析】
(1) 过点![]() 作
作![]() ∥
∥![]() ,则
,则![]() ∥
∥![]() ,根据平行线的性质可得
,根据平行线的性质可得![]() ,
, ![]() ,从而可证结论成立;
,从而可证结论成立;
(2)过点![]() 作
作![]() ∥
∥![]() ,可证
,可证![]() ,由
,由![]() 平分
平分![]() ,可证
,可证![]() ,从而
,从而![]() ,由
,由![]() ∥
∥![]() 可证
可证![]() ,从而
,从而 ![]() ,结合
,结合![]() ,可求出结论;
,可求出结论;
(3)由AB∥CD,可证∠BEH=∠EFG,从而∠AEP=180°-2∠EFG①,由三角形外角的性质得,∠EFG=∠EHG+∠HGF=EHG+![]() ∠CGP②,由①和②可得,∠AEP+∠CGP=180°-2∠EHG,又由(1)知,∠EPG=∠AEP+∠PGC,从而∠EPG=1800-2∠EHG .
∠CGP②,由①和②可得,∠AEP+∠CGP=180°-2∠EHG,又由(1)知,∠EPG=∠AEP+∠PGC,从而∠EPG=1800-2∠EHG .
(1) 过点![]() 作
作![]() ∥
∥![]() ,
,
∵ ![]()
![]() ,
,
∴![]() ∥
∥![]() ,
,
∴ ![]() ,
, ![]() ,
,
∴ ∠EPG=∠AEP+∠PGC ;

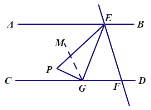
(2)过点![]() 作
作![]() ∥
∥![]() ,
,
 1
1
∴ ![]() ,
,
![]() ,
,
∴ ![]() ,
,
∵![]() 平分
平分![]() ,
,
∴ ![]() ,
,
∴![]() .
.
∵ ![]() ,
,
又∵ ![]() ∥
∥![]() ,
,
∴ ![]() ,
,
即![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() ,
,
(3)∠EPG=1800-2∠EHG .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】【定义】已知P为△ABC所在平面内一点,连接PA,PB,PC,在△PAB,△PBC和△PAC中,若存在一个三角形与△ABC相似(全等除外),那么就称P为△ABC的“共相似点”,根据“共相似点”是否落在三角形的内部,边上或外部,可将其分为“内共相似点”,“边共相似点”或“外共相似点”.
(1)据定义可知,等边三角形(填“存在”或“不存在”)共相似点.
(2)如图1,若△ABC的一个边共相似点P与其对角顶点B的连线,将△ABC分割成的两个三角形恰与原三角形均相似,试判断△ABC的形状,并说明理由.
(3)如图2,在△ABC中,∠A<∠B<∠C,高线CD与角平分线BE交于点P,若P是△ABC的一个内共相似点,试说明点E是△ABC的边共相似点,并直接写出∠A的度数.
(4)如图3,在Rt△ABC中,∠C=90°,∠A=30°,BC= ,若△PBC与△ABC相似,则满足条件的P点共有个,顺次连接所有满足条件的P点而围成的多边形的周长为 .
,若△PBC与△ABC相似,则满足条件的P点共有个,顺次连接所有满足条件的P点而围成的多边形的周长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=40°,∠C=80°,AD是BC边上的高,AE平分∠BAC.
(1)求∠BAE的度数;(2)求∠DAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )

A.2
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半.
(1)求这个多边形是几边形;
(2)求这个多边形的每一个内角的度数.
相关试题

