【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.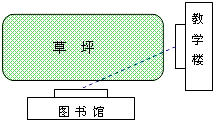
情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由: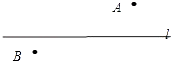
你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
参考答案:
【答案】解:情景一:因为教学楼和图书馆处于同一条直线上,两点之间的所有连线中,线段最短,所以这样走比较近;
情景二:抽水站点P的位置如右图所示:
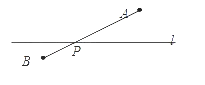
理由:两点之间的所有连线中,线段最短;
赞同情景二中运用知识的做法,应用数学知识为人类服务时应注意:不能以破坏环境为代价..
【解析】(1)把教学楼看成一个点,图书室也看成一个点,根据连接两点的所有线中,线段最短;
(2)连接AB交直线L于点P,点P 就是抽水站点的位置,根据连接两点的所有线中,线段最短;第二问其实就是一个学生道德情感教育的题,赞同情景二中运用知识的做法,应用数学知识为人类服务时应注意:不能以破坏环境为代价.
-
科目: 来源: 题型:
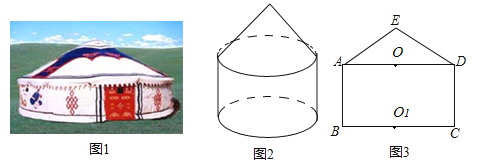
查看答案和解析>>【题目】图(1)是一个蒙古包的照片,这个蒙古包可以近似看成是圆锥和圆柱组成的几何体,如图(2)所示.
(1)请画出这个几何体的俯视图;
(2)图(3)是这个几何体的正面示意图,已知蒙古包的顶部离地面的高度EO1=6米,圆柱部分的高OO1=4米,底面圆的直径BC=8米,求∠EAO的度数(结果精确到0.1°).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)已知关于x的方程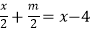 与方程
与方程 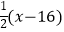 =x-6的解相同,求m的值.
=x-6的解相同,求m的值.
(2)如果关于x的方程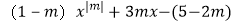 =0是一元一次方程,求此方程的解
=0是一元一次方程,求此方程的解 -
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,∠A+∠C=270°,则∠B=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(﹣3,2)重合,则点A的坐标是( )
A.(2,5)
B.(﹣8,5)
C.(﹣8,﹣1)
D.(2,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如果电梯上升5层记为+5.那么电梯下降2层应记为( )
A. +2 B. ﹣2 C. +5 D. ﹣5
相关试题

