【题目】数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
(1)探究一:求不等式|x﹣1|<2的解集
探究|x﹣1|的几何意义
如图①,在以O为原点的数轴上,设点A′对应的数是x﹣1,有绝对值的定义可知,点A′与点O的距离为|x﹣1|,可记为A′O=|x﹣1|.将线段A′O向右平移1个单位得到线段AB,此时点A对应的数是x,点B对应的数是1.因为AB=A′O,所以AB=|x﹣1|,因此,|x﹣1|的几何意义可以理解为数轴上x所对应的点A与1所对应的点B之间的距离AB.
探究求方程|x﹣1|=2的解
因为数轴上3和﹣1所对应的点与1所对应的点之间的距离都为2,所以方程的解为3,﹣1.
探究:
求不等式|x﹣1|<2的解集
因为|x﹣1|表示数轴上x所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点对应的数x的范围.
请在图②的数轴上表示|x﹣1|<2的解集,并写出这个解集.
(2)探究二:探究 ![]() 的几何意义
的几何意义
探究:![]() 的几何意义
的几何意义
如图③,在直角坐标系中,设点M的坐标为(x,y),过M作MP⊥x轴于P,作MQ⊥y轴于Q,则P点坐标为(x,0),Q点坐标为(0,y),OP=|x|,OQ=|y|,在Rt△OPM中,PM=OQ=|y|,则MO= ![]() =
= ![]() =
= ![]() ,因此,
,因此, ![]() 的几何意义可以理解为点M(x,y)与点O(0,0)之间的距离MO.
的几何意义可以理解为点M(x,y)与点O(0,0)之间的距离MO.
探究:![]() 的几何意义
的几何意义
如图④,在直角坐标系中,设点A′的坐标为(x﹣1,y﹣5),由探究二(1)可知,A′O= ![]() ,将线段A′O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时点A的坐标为(x,y),点B的坐标为(1,5),因为AB=A′O,所以AB=
,将线段A′O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时点A的坐标为(x,y),点B的坐标为(1,5),因为AB=A′O,所以AB= ![]() ,因此
,因此 ![]() 的几何意义可以理解为点A(x,y)与点B(1,5)之间的距离AB.
的几何意义可以理解为点A(x,y)与点B(1,5)之间的距离AB.
探究 ![]() 的几何意义
的几何意义
①请仿照探究二的方法,在图⑤中画出图形,并写出探究过程.
② ![]() 的几何意义可以理解为:
的几何意义可以理解为:
(3)拓展应用:
① ![]() +
+ ![]() 的几何意义可以理解为:点A(x,y)与点E(2,﹣1)的距离和点A(x,y)与点F(填写坐标)的距离之和.
的几何意义可以理解为:点A(x,y)与点E(2,﹣1)的距离和点A(x,y)与点F(填写坐标)的距离之和.
② ![]() +
+ ![]() 的最小值为(直接写出结果)
的最小值为(直接写出结果)
参考答案:
【答案】
(1)
解:如图所示,
![]()
∴|x﹣1|<2的解集是﹣1<x<3,
(2)
解:① ![]() 的几何意义是:点A(x,y)与B(﹣3,4)之间的距离,
的几何意义是:点A(x,y)与B(﹣3,4)之间的距离,
∴过点B作BD⊥x轴于D,过点A作AC⊥BD于点C,
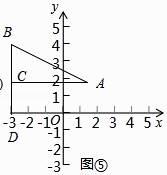
∴AC=|x+3|,BC=|y﹣4| ![]() ,
,
∴由勾股定理可知:AB2=AC2+BC2,
∴AB= ![]() ,
,
②点(x,y)与点(a,b)之间的距离
(3)(﹣1,﹣5);5
【解析】解:
【答案】解:如图所示, ![]()
∴|x﹣1|<2的解集是﹣1<x<3,
拓展研究:(1)由探究二(4)可知 ![]() 表示点(x,y)与(﹣1,﹣5)之间的距离,
表示点(x,y)与(﹣1,﹣5)之间的距离,
故F(﹣1,﹣5),(2)由(1)可知: ![]() +
+ ![]() 表示点A(x,y)与点E(2,﹣1)的距离和点A(x,y)与点F(﹣1,﹣5)的距离之和,
表示点A(x,y)与点E(2,﹣1)的距离和点A(x,y)与点F(﹣1,﹣5)的距离之和,
当A(x,y)位于直线EF外时,
此时点A、E、F三点组成△AEF,
∴由三角形三边关系可知:EF<AF+AE,
当点A位置线段EF之间时,此时EF=AF+AE,
∴ ![]() +
+ ![]() 的最小值为EF的距离,
的最小值为EF的距离,
∴EF= ![]() =5
=5
所以答案是:探究二(4)点(x,y)与点(a,b)之间的距离;
拓展研究(1)(﹣1,﹣5);(2)5.![]()
【考点精析】利用两点间的距离对题目进行判断即可得到答案,需要熟知同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发,图中l1 , l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:

(1)表示乙离A地的距离与时间关系的图象是(填l1或l2); 甲的速度是km/h,乙的速度是km/h;
(2)甲出发多少小时两人恰好相距5km? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
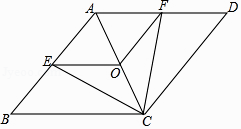
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间价格比淡季上涨
 .下表是去年该酒店豪华间某两天的相关记录:
.下表是去年该酒店豪华间某两天的相关记录: 淡季
旺季
未入住房间数
10
0
日总收入(元)
24000
40000
(1)该酒店豪华间有多少间?旺季每间价格为多少元?
(2)今年旺季来临,豪华间的间数不变.经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加25元,每天未入住房间数增加1间.不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:Rt△EFP和矩形ABCD如图①摆放(点P与点B重合),点F,B(P),C在同一直线上,AB=EF=6cm,BC=FP=8cm,∠EFP=90°,如图②,△EFP从图①的位置出发,沿BC方向匀速运动,速度为1cm/s,EP与AB交于点G;同时,点Q从点C出发,沿CD方向匀速运动,速度为1cm/s.过点Q作QM⊥BD,垂足为H,交AD于点M,连接AF,FQ,当点Q停止运动时,△EFQ也停止运动.设运动时间为t(s)(0<t<6),解答下列问题:

(1)当t为何值时,PQ∥BD?
(2)设五边形AFPQM的面积为y(cm2),求y与t之间的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S五边形AFPQM:S矩形ABCD=9:8?若存在,求出t的值;若不存在,请说明理由.
(4)在运动过程中,是否存在某一时刻t,使点M在线段PG的垂直平分线上?若存在,求出t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论: ①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )
A.①②③④
B.②③
C.①②④
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )

A.
B.
C.
D.
相关试题

