【题目】如图,在同一平面内四个点A,B,C,D.
(1)利用尺规,按下面的要求作图.要求:不写画法,保留作图痕迹,不必写结论.
①作射线AC;
②连接AB,BC,BD,线段BD与射线AC相交于点O;
③在线段AC上作一条线段CF,使CF=AC﹣BD.
(2)观察(1)题得到的图形,我们发现线段AB+BC>AC,得出这个结论的依据是 .
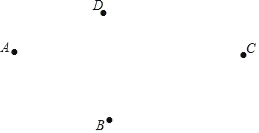
参考答案:
【答案】(1)①如图所示,射线AC即为所求,见解析;②如图所示,线段AB,BC,BD即为所求,见解析;③如图所示,线段CF即为所求,见解析;(2)根据两点之间,线段最短.
【解析】
(1)①连接AC并延长即可;②连接AB,BC,BD即可;③以点A为圆心,BD长为半径画弧交AC于F,则线段CF=AC-BD;
(2)根据两点之间,线段最短,可得AB+BC>AC.
(1)①如图所示,射线AC即为所求;
②如图所示,线段AB,BC,BD即为所求;
③如图所示,线段CF即为所求;
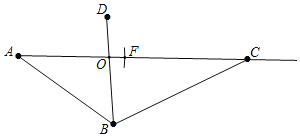
(2)根据两点之间,线段最短,可得AB+BC>AC.
故答案为:两点之间,线段最短.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点D是△ABC所在平面内一点,连接AD、CD.
(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;
(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;
(3)如图3,在 (2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=90°,点D为AC上一动点.
(1)如图1,点E、点F均是射线BD上的点并且满足AE=AF,∠EAF=90°.求证:△ABE≌△ACF;
(2)在(1)的条件下,求证:CF⊥BD;
(3)由(1)我们知道∠AFB=45°,如图2,当点D的位置发生变化时,过点C作CF⊥BD于F,连接AF.那么∠AFB的度数是否发生变化?请证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求进行计算:
(1)计算: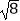 +(﹣2017)0﹣4sin45°
+(﹣2017)0﹣4sin45°
(2)化简:m(1﹣m)+(m﹣2)2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标是(0,6),点B的坐标是(6,0).
(1)如图1,点C的坐标是(﹣2,0),BD⊥AC于D交y轴于点E.求点E的坐标;
(2)在(1)的条件下求证:OD平分∠CDB;
(3)如图2,点F为AB中点,点G为x正半轴点B右侧一动点,过点F作FG的垂线FH,交y轴的负半轴于点H,那么当点G的位置不断变化时,S△AFH﹣S△FBG的值是否发生变化?若变化,请说明理由;若不变化,请求出相应结果.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c是△ABC的三边,若a,b,c满足a2-6a+b2-8b+
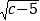 +25=0,则△ABC是_____________三角形;若a,b,c满足a2+b2+c2-ab-bc-ac=0,则△ABC是_________三角形.
+25=0,则△ABC是_____________三角形;若a,b,c满足a2+b2+c2-ab-bc-ac=0,则△ABC是_________三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4
∵(y+2)2≥0
∴(y+2)2+4≥4
∴y2+4y+8的最小值是4.
(1)求代数式m2+m+4的最小值;
(2)求代数式4﹣x2+2x的最大值;
(3)某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?

相关试题

