【题目】在△ABC中,AB=AC,∠BAC=90°,点D为AC上一动点.
(1)如图1,点E、点F均是射线BD上的点并且满足AE=AF,∠EAF=90°.求证:△ABE≌△ACF;
(2)在(1)的条件下,求证:CF⊥BD;
(3)由(1)我们知道∠AFB=45°,如图2,当点D的位置发生变化时,过点C作CF⊥BD于F,连接AF.那么∠AFB的度数是否发生变化?请证明你的结论.

参考答案:
【答案】(1)详见解析;(2)详见解析;(3)∠AFB=45°不变化,理由详见解析.
【解析】
(1)易得∠BAE=∠CAF,由已知AB=AC、AE=AF,可得△ABE≌△ACF;
(2)由题意得∠ABE+∠BDA=90°,由(1)得∠ABE=∠ACF,又∠BDA=∠CDF,可得答案;
(3) ∠AFB=45°不变化,理由如下:过点A作AF的垂线交BM于点E,可证得△ABE≌△ACF,可得AE=AF,△AEF是等腰直角三角形,∠AFB=45°.
(1)∵∠BAC=∠BAE+∠EAD=90°,∠EAF=∠CAF+∠EAD=90°
∴∠BAE=∠CAF
在△ABE和△ACF中

∴△ABE≌△ACF(SAS)
(2)∵∠BAC=90°
∴∠ABE+∠BDA=90°,
由(1)得△ABE≌△ACF
∴∠ABE=∠ACF
∴∠BDA+∠ACF=90°
又∵∠BDA=∠CDF
∴∠CDF+∠ACF=90°
∴∠BFC=90°
∴CF⊥BD
(3)∠AFB=45°不变化,理由如下:
过点A作AF的垂线交BM于点E

∵CF⊥BD
∴∠BAC=90°
∴∠ABD+∠BDA=90°
同理∠ACF+∠CDF=90°
∵∠CDF=∠ADB
∴∠ABD=∠ACF
同(1)理得∠BAE=∠CAF
在△ABE和△ACF中

∴△ABE≌△ACF(ASA)
∴AE=AF
∴△AEF是等腰直角三角形
∴∠AFB=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某体育用品商店,购买50根跳绳和80个毽子共用1120元,购买30根跳绳和50个毽子共用680元.
(1)跳绳、毽子的单价各是多少元?
(2)该店在“元旦”节期间开展促销活动,所有商品按同样的折数打折销售.节日期间购买100根跳绳和100个毽子只需1700元,该店的商品按原价的几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】【提出问题】如图1,小东将一张AD为12,宽AB为4的长方形纸片按如下方式进行折叠:在纸片的一边BC上分别取点P、Q,使得BP=CQ,连结AP、DQ,将△ABP、△DCQ分别沿AP、DQ折叠得△APM,△DQN,连结MN.小东发现线段MN的位置和长度随着点P、Q的位置发生改变.
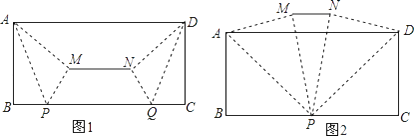
(1)【规律探索】请在图1中过点M,N分别画ME⊥BC于点E,NF⊥BC于点F.
求证:①ME=NF;②MN∥BC.
(2)【解决问题】如图1,若BP=3,求线段MN的长;
(3)如图2,当点P与点Q重合时,求MN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点D是△ABC所在平面内一点,连接AD、CD.
(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;
(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;
(3)如图3,在 (2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求进行计算:
(1)计算: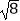 +(﹣2017)0﹣4sin45°
+(﹣2017)0﹣4sin45°
(2)化简:m(1﹣m)+(m﹣2)2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一平面内四个点A,B,C,D.
(1)利用尺规,按下面的要求作图.要求:不写画法,保留作图痕迹,不必写结论.
①作射线AC;
②连接AB,BC,BD,线段BD与射线AC相交于点O;
③在线段AC上作一条线段CF,使CF=AC﹣BD.
(2)观察(1)题得到的图形,我们发现线段AB+BC>AC,得出这个结论的依据是 .
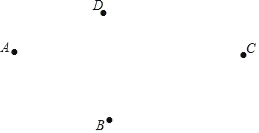
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标是(0,6),点B的坐标是(6,0).
(1)如图1,点C的坐标是(﹣2,0),BD⊥AC于D交y轴于点E.求点E的坐标;
(2)在(1)的条件下求证:OD平分∠CDB;
(3)如图2,点F为AB中点,点G为x正半轴点B右侧一动点,过点F作FG的垂线FH,交y轴的负半轴于点H,那么当点G的位置不断变化时,S△AFH﹣S△FBG的值是否发生变化?若变化,请说明理由;若不变化,请求出相应结果.

相关试题

