Question

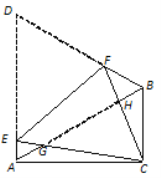
【题目】如图，在△ABC中，∠ACB=90°，∠CAB=30°, △ABD是等边三角形，将四边形ACBD沿直线EF折叠，使D与C重合，CE与CF分别交AB于点G、H.

（1）求证：△AEG∽△CHG；

（2）△AEG与△BHF是否相似，并说明理由；

（3）若BC=1，求cos∠CHG的值.

Answer 1

【答案】（1）证明见解析（2）△AEG与△BHF相似 （3）

【解析】试题分析：（1）由于△ABD是等边三角形，那么∠D=∠EAG=60°，根据折叠的性质知：∠D=∠GCH=∠AEG=60°，再加上对顶角∠EGA=∠HGC，即可证得所求的三角形相似；

（2）由△ABD是等边三角形和的性质知：∠BAD=∠GCH=∠ABD，再由三角形内角和定理可证明∠1=∠5，即可得到结论；

（3）在Rt△ABC中，已知了BC的长和∠BAC的度数，即可求得AB、AC的值，由折叠的性质知：DE=CE，可设出DE、CE的长，然后表示出AE的长，进而可在Rt△AEC中，由勾股定理求得AE、CE的值，即可得到∠AEG的余弦值，而根据（1）的相似三角形知∠AEG=∠CHG，由此得解．

试题解析：解：（1）∵△ABD是等边三角形，∴∠EAG=∠D=60°；

根据折叠的性质知：DE=CE，∠D=∠GCH=∠EAG=60°，又∵∠EGA=∠HGC，∴△AEG∽△CHG．

（2）△AEG与△BHF相似．理由如下：

∵∠BAD=∠ABD=∠D，∠GCH=∠D，∴∠BAD=∠GCH=∠ABD，∴∠1+∠2=∠3+∠4．∵∠2=∠3，∠4=∠5，∴∠1=∠5， ∴△AEG∽△BHF；

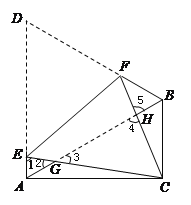
（3）△ABC中，∠BAC=30°，BC=1，则AC=，AB=2，故AD=AB=2．

设DE=EC=x，则AE=2﹣x．

在Rt△AEC中，由勾股定理，得：（2﹣x）2+3=x2，解得x=，∴AE=，EC=，∴cos∠AEC==．由（1）的相似三角形知：∠AEG=∠CHG，故cos∠CHG=cos∠AEC=．