【题目】已知![]() 是最大的负整数,且
是最大的负整数,且![]() ,
,![]() ,
,![]() 满足
满足![]() ,请回答下列问题.
,请回答下列问题.
(1)请直接写出![]() ,
,![]() ,
,![]() 的值.
的值.
(2)若![]() 为数轴上一动点,其对应的数为
为数轴上一动点,其对应的数为![]() ,点
,点![]() 在0到1之间运动时(即
在0到1之间运动时(即![]() ),请化简式子:
),请化简式子:![]() .
.
(3)若![]() ,
,![]() ,
,![]() 在数轴上据对应的点分别为
在数轴上据对应的点分别为![]() ,
,![]() ,
,![]() .点
.点![]() ,
,![]() ,
,![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒2个单位长度的速度向左运动,同时点
以每秒2个单位长度的速度向左运动,同时点![]() 和点
和点![]() 分别以每秒3个单位长度和每秒8个单位长度的速度向右运动,若点
分别以每秒3个单位长度和每秒8个单位长度的速度向右运动,若点![]() 和点
和点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() ,点
,点![]() 之间的距离表示为
之间的距离表示为![]() ,设运动时间为
,设运动时间为![]() ,要使
,要使![]() 的值不变,请直接写出此时
的值不变,请直接写出此时![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)要使
;(3)要使![]() 的值不变,t的取值范围为
的值不变,t的取值范围为![]() .
.
【解析】
(1)先根据负整数的性质可求出b的值,再根据绝对值和偶次方的非负性得出等式求解即可得;
(2)先将题(1)的结论代入所需化简的式子,再根据绝对值运算化简即可得;
(3)先根据运动时间求出运动过程中,点![]() 对应的数,从而可得
对应的数,从而可得![]() 的值,再根据其值与时间t无关即可得出答案.
的值,再根据其值与时间t无关即可得出答案.
(1)![]() 是最大的负整数
是最大的负整数
![]()
![]() ,即
,即![]()
![]()
解得![]()
故![]() ;
;
(2)由(1)得:![]()
![]()
![]()
![]()
![]()
![]()
![]()
即![]() ;
;
(3)由题意得:运动过程中,点A对应的数为![]() ,点B对应的数为
,点B对应的数为![]() ,点C对应的数为
,点C对应的数为![]()
因点C在点B右侧,且点C运动速度大于点B运动速度,则点C一定在点B前面,![]()
![]()
则![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
故要使![]() 的值不变,t的取值范围为
的值不变,t的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人去年水果批发市场采购苹果,他看中了
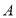 、
、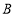 两家苹果.这两家苹果品质一样,零售价都为6元/千克,批发价各不相同.
两家苹果.这两家苹果品质一样,零售价都为6元/千克,批发价各不相同.(1)
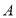 家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量超过1000千克且不超过2000千克,所有苹果按零售价的90%优惠;超过2000千克,所有苹果按零售价的88%优惠.
家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量超过1000千克且不超过2000千克,所有苹果按零售价的90%优惠;超过2000千克,所有苹果按零售价的88%优惠.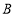 家的规定如下表:
家的规定如下表:数量范围(千克)
0—500
500以上—1500
1500以上—2500
2500以上
价格(元)
零售价的95%
零售价的85%
零售价的75%
零售价的70%
表格说明:批发价格分段计算,如某人批发苹果2100千克,则总费用=6×95%×500+6×85%×1000+6×75%×(2100-1500).
(1)如果他批发600千克苹果,那么他在
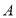 、
、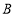 两家批发分别需要多少元?
两家批发分别需要多少元?(2)如果他批发
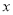 千克苹果(1500<
千克苹果(1500<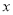 <2000),请你分别用含
<2000),请你分别用含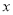 的代数式表示在
的代数式表示在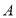 、
、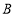 两家批发所需的费用.
两家批发所需的费用.(3)现在他要批发1800千克苹果,选择在哪家批发更优惠呢?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,AB∥CD,∠A=90
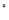 ,AB=
,AB=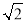 ,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△CDE的面积为_____.
,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△CDE的面积为_____.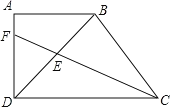
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过一年多的精准帮扶,小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国,小明家网店中红枣和小米这两种商品的相关信息如下表:
商品
红枣
小米
规格
1kg/袋
2kg/袋
成本(元/袋)
40
38
售价(元/袋)
60
54
根据上表提供的信息,解答下列问题:
(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共3000kg,获得利润4.2万元,求这前五个月小明家网店销售这种规格的红枣多少袋;
(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共2000kg,其中,这种规格的红枣的销售量不低于600kg.假设这后五个月,销售这种规格的红枣味x(kg),销售这种规格的红枣和小米获得的总利润为y(元),求出y与x之间的函数关系式,并求出这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在复习课上,wsy老师要求写出几个与实数有关的结论:小明同学写了以下5个:
①任何无理数都是无限不循环小数;
②有理数与数轴上的点一一对应;
③在1和3之间的无理数有且只有
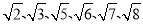 这5个;
这5个;④
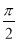 是分数,它是有理数;
是分数,它是有理数;⑤由四舍五入得到的近似数7.30表示大于或等于7.295,而小于7.305的数.其中正确的个数是( )
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.
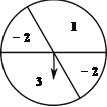
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC、BC相交于点M、N.
(1)过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;
(2)连接MD,求证:MD=NB.
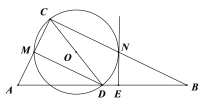
相关试题

