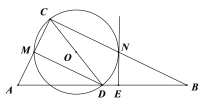
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC、BC相交于点M、N.
(1)过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;
(2)连接MD,求证:MD=NB.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】(1)如图,连接ON,根据直角三角形斜边中线等于斜边的一半可得AD=CD=DB,从而可得∠DCB=∠DBC,再由∠DCB=∠ONC,可推导得出ON∥AB,再结合NE是⊙O的切线,ON//AB,继而可得到结论;
(2)如图,由(1)可知ON∥AB,继而可得N为BC中点,根据圆周角定理可知∠CMD=90°,继而可得MD∥CB,再由D是AB的中点,根据得到MD=NB.
(1)如图,连接ON,
∵CD是Rt△ABC斜边AB上的中线,
∴AD=CD=DB,
∴∠DCB=∠DBC,
又∵OC=ON,∴∠DCB=∠ONC,
∴∠ONC=∠DBC,
∴ON∥AB,
∵NE是⊙O的切线,ON是⊙O的半径,
∴∠ONE=90°,
∴∠NEB=90°,即NE⊥AB;
(2)如图所示,由(1)可知ON∥AB,
∵OC=OD,∴
∴CN=NB=![]() CB,
CB,
又∵CD是⊙O的直径,∴∠CMD=90°,
∵∠ACB=90°,
∴∠CMD+∠ACB=180°,∴MD//BC,
又∵D是AB的中点,∴MD=![]() CB,
CB,
∴MD=NB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
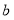 是最大的负整数,且
是最大的负整数,且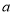 ,
,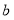 ,
,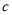 满足
满足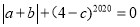 ,请回答下列问题.
,请回答下列问题.(1)请直接写出
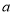 ,
,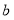 ,
,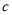 的值.
的值.(2)若
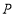 为数轴上一动点,其对应的数为
为数轴上一动点,其对应的数为 ,点
,点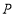 在0到1之间运动时(即
在0到1之间运动时(即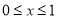 ),请化简式子:
),请化简式子: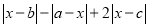 .
.(3)若
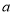 ,
,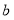 ,
,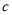 在数轴上据对应的点分别为
在数轴上据对应的点分别为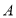 ,
,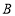 ,
,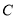 .点
.点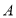 ,
,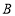 ,
,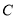 开始在数轴上运动,若点
开始在数轴上运动,若点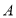 以每秒2个单位长度的速度向左运动,同时点
以每秒2个单位长度的速度向左运动,同时点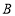 和点
和点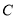 分别以每秒3个单位长度和每秒8个单位长度的速度向右运动,若点
分别以每秒3个单位长度和每秒8个单位长度的速度向右运动,若点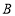 和点
和点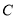 之间的距离表示为
之间的距离表示为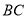 ,点
,点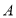 ,点
,点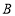 之间的距离表示为
之间的距离表示为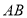 ,设运动时间为
,设运动时间为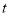 ,要使
,要使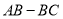 的值不变,请直接写出此时
的值不变,请直接写出此时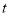 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在复习课上,wsy老师要求写出几个与实数有关的结论:小明同学写了以下5个:
①任何无理数都是无限不循环小数;
②有理数与数轴上的点一一对应;
③在1和3之间的无理数有且只有
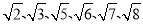 这5个;
这5个;④
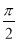 是分数,它是有理数;
是分数,它是有理数;⑤由四舍五入得到的近似数7.30表示大于或等于7.295,而小于7.305的数.其中正确的个数是( )
A.1B.2C.3D.4
-
科目: 来源: 题型:
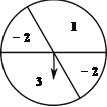
查看答案和解析>>【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边三角形ABC的顶点B、C的坐标分别为(0,0)和(0,4).
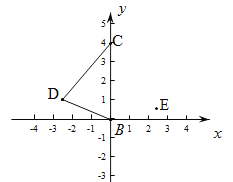
(1)求顶点A的坐标.
(2)D为第二象限内一点,作出点P,使得P到DB和DC的距离相等,且到点E的距离等于DB(不写作法,保留作图痕迹).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示的方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过2017次运动后,动点P的坐标为( )
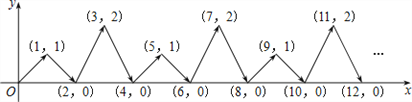
A. (2017,1) B. (2017,0) C. (2017,2) D. (2016,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,∠BAC=150
 ,∠CAD=120
,∠CAD=120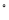 .求证:AC=2AD.
.求证:AC=2AD.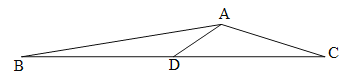
相关试题

