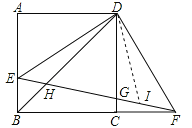
【题目】如图,正方形ABCD中,E为AB边上一点,过点D作DF⊥DE,与BC延长线交于点F.连接EF,与CD边交于点G,与对角线BD交于点H.
(1)若BF=BD=![]() ,求BE的长;
,求BE的长;
(2)若∠ADE=2∠BFE,求证:FH=HE+HD.

参考答案:
【答案】(1)BE=2-![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】分析:(1)由四边形ABCD正方形,BF=BD=![]() ,由勾股定理即可求得BC的长,又由DF⊥DE,易证得△ADE≌△CDF,即可求得BE的长;
,由勾股定理即可求得BC的长,又由DF⊥DE,易证得△ADE≌△CDF,即可求得BE的长;
(2)首先在FE上截取一段FI,使得FI=EH,由△ADE≌△CDF,易证得△DEH≌△DFI,即可得DH=DI,又由∠ADE=2∠BFE,易证得△DHI为等边三角形,即可得DH=HI,继而可得FH=HE+HD.
详解:(1)解:∵四边形ABCD正方形,∴∠BCD=90°,BC=CD,∴Rt△BCD中,BC2+CD2=BD2,即BC2=(![]() )2﹣(BC)2,∴BC=AB=1.∵DF⊥DE,∴∠ADE+∠EDC=90°=∠EDC+∠CDF,∴∠ADE=∠CDF.在△ADE和△CDF中,∵
)2﹣(BC)2,∴BC=AB=1.∵DF⊥DE,∴∠ADE+∠EDC=90°=∠EDC+∠CDF,∴∠ADE=∠CDF.在△ADE和△CDF中,∵ ,∴△ADE≌△CDF(ASA),∴AE=CF=BF﹣BC=
,∴△ADE≌△CDF(ASA),∴AE=CF=BF﹣BC=![]() ﹣1,∴BE=AB﹣AE=1﹣(
﹣1,∴BE=AB﹣AE=1﹣(![]() ﹣1)=2﹣
﹣1)=2﹣![]() ;
;
(2)证明:在FE上截取一段FI,使得FI=EH.∵△ADE≌△CDF,∴DE=DF,∴△DEF为等腰直角三角形,∴∠DEF=∠DFE=45°=∠DBC.∵∠DHE=∠BHF,∴∠EDH=∠BFH(三角形的内角和定理).在△DEH和△DFI中,∵ ,∴△DEH≌△DFI(SAS),∴DH=DI.又∵∠HDE=∠BFE,∠ADE=2∠BFE,∴∠HDE=∠BFE=
,∴△DEH≌△DFI(SAS),∴DH=DI.又∵∠HDE=∠BFE,∠ADE=2∠BFE,∴∠HDE=∠BFE=![]() ∠ADE.∵∠HDE+∠ADE=45°,∴∠HDE=15°,∴∠DHI=∠DEH+∠HDE=60°,即△DHI为等边三角形,∴DH=HI,∴FH=FI+HI=HE+HD.
∠ADE.∵∠HDE+∠ADE=45°,∴∠HDE=15°,∴∠DHI=∠DEH+∠HDE=60°,即△DHI为等边三角形,∴DH=HI,∴FH=FI+HI=HE+HD.
-
科目: 来源: 题型:
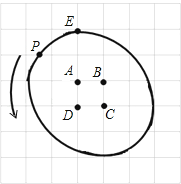
查看答案和解析>>【题目】在每个小正方形的边长均为1的7×7网格图中,格点上有A,B,C,D,E五个定点,如图所示,一个动点P从点E出发,绕点A逆时针旋转90°,之后该动点继续绕点B,C,D逆时针90°后回到初始位置,点P运转路线的总长是 . (结果保留π)
-
科目: 来源: 题型:
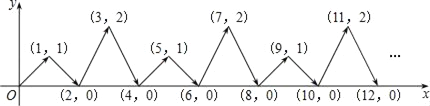
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2016次运动后,动点P的坐标是( )
A. (2016,1) B. (2016,0) C. (2016,2) D. (2017,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正三角形和正方形的面积分别为10,6,两阴影部分的面积分别为a,b(a>b),则(a﹣b)等于 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为
 ,C点的坐标为
,C点的坐标为 ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着 的路线移动
的路线移动 即:沿着长方形移动一周
即:沿着长方形移动一周 .
. 写出点B的坐标
写出点B的坐标 ______
______
 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标. 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90°,且AD=12cm,AB=8cm,DC=10cm,若动点P从A点出发,以每秒2cm的速度沿线段AD向点D运动;动点Q从C点出发以每秒3cm的速度沿CB向B点运动,当P点到达D点时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:
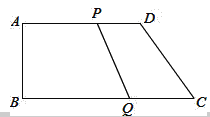
(1)BC= cm;
(2)当t为多少时,四边形PQCD成为平行四边形?
(3)当t为多少时,四边形PQCD为等腰梯形?
(4)是否存在t,使得△DQC是等腰三角形?若存在,请求出t的值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.

试说明:AC∥DF.
相关试题

