【题目】如图1,在△ABC中,AB=BC,点D、E分别在边BC,AC上,连接DE,且DE=DC.

(1)问题发现:若∠ACB=∠ECD=45°,则![]() = .
= .
(2)拓展探究:若∠ACB=∠ECD=30°,将△EDC饶点C按逆时针旋转α度(0°<α<180°),图2是旋转过程中的某一位置,在此过程中![]() 的大小有无变化?如果不变,请求出
的大小有无变化?如果不变,请求出![]() 的值,如果变化,请说明理由;
的值,如果变化,请说明理由;
(3)问题解决:若∠ABC=∠EDC=β(0°<β<90°),将△EDC旋转到如图3所示的位置时,则![]() 的值为 .(用含β的式子表示)
的值为 .(用含β的式子表示)
参考答案:
【答案】(1)![]() ;(2)不变化,理由详见解析;(3)2cosβ.
;(2)不变化,理由详见解析;(3)2cosβ.
【解析】
(1)如图1,过E作EF⊥AB于F,根据等腰三角形的性质得到∠A=∠C=∠DEC=45°,于是得到∠B=∠EDC=90°,推出四边形EFBD是矩形,得到EF=BD,推出△AEF是等腰直角三角形,根据等腰直角三角形的性质得到结论;
(2)根据等腰三角形的性质得到∠ACB=∠CAB=∠ECD=∠CED=30°,根据相似三角形的判定和性质即可得到结论;
(3)根据等腰三角形的性质得到∠ACB=∠CAB=∠ECD=∠CED=β,根据相似三角形的性质得到![]() ,即
,即![]() ,根据角的和差得到∠ACE=∠BCD,求得△ACE∽△BCD,证得
,根据角的和差得到∠ACE=∠BCD,求得△ACE∽△BCD,证得![]() ,过点B作BF⊥AC于点F,则AC=2CF,根据相似三角形的性质即可得到结论.
,过点B作BF⊥AC于点F,则AC=2CF,根据相似三角形的性质即可得到结论.
解:(1)如图1,过E作EF⊥AB于F,
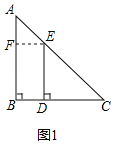
∵BA=BC,DE=DC,∠ACB=∠ECD=45°,
∴∠A=∠C=∠DEC=45°,
∴∠B=∠EDC=90°,
∴四边形EFBD是矩形,
∴EF=BD,
∴EF∥BC,
∴△AEF是等腰直角三角形,
∴![]() ,
,
故答案为:![]() ;
;
(2)此过程中![]() 的大小有变化,
的大小有变化,
由题意知,△ABC和△EDC都是等腰三角形,
∴∠ACB=∠CAB=∠ECD=∠CED=30°,
∴△ABC∽△EDC,
∴![]() ,即
,即![]() ,
,
又∠ECD+∠ECB=∠ACB+∠ECB,
∴∠ACE=∠BCD,
∴△ACE∽△BCD,
∴![]() ,
,
在△ABC中,如图2,过点B作BF⊥AC于点F,
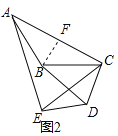
则AC=2CF,
在Rt△BCF中,CF=BCcos30°=![]() BC,
BC,
∴AC=![]() BC.
BC.
∴![]() =
=![]() ;
;
(3)由题意知,△ABC和△EDC都是等腰三角形,且∠ACB=∠ECD=β,
∴∠ACB=∠CAB=∠ECD=∠CED=β,
∴△ABC∽△EDC,
∴![]() ,即
,即![]() ,
,
又∠ECD+∠ECB=∠ACB+∠ECB,
∴∠ACE=∠BCD,
∴△ACE∽△BCD,
∴![]() ,
,
在△ABC中,如图3,过点B作BF⊥AC于点F,则AC=2CF,
在Rt△BCF中,CF=BCcosβ,
∴AC=2BCcosβ.
∴![]() =2cosβ,
=2cosβ,
故答案为2cosβ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
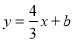 与
与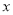 轴交于点
轴交于点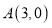 ,与
,与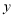 轴交于点
轴交于点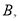 将
将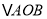 沿
沿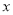 轴折叠,使点
轴折叠,使点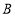 落在
落在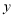 轴的点
轴的点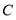 上,设
上,设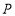 为线段
为线段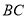 上的一个动点,点
上的一个动点,点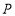 与点
与点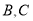 不重合,连接
不重合,连接 .以点
.以点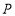 为端点作射线
为端点作射线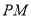 交线段
交线段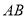 于点
于点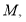 使
使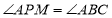 .
.
 求点
求点 的坐标;
的坐标;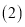 当
当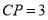 时,求直线
时,求直线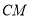 的解析式;
的解析式;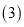 是否存在点
是否存在点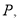 使
使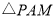 为直角三角形?若存在,请直接写出点
为直角三角形?若存在,请直接写出点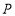 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线BD平分
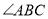 ,
,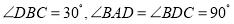 ,E为BC的中点,AE与BD相交于点F,若
,E为BC的中点,AE与BD相交于点F,若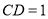 ,则BF的长为( )
,则BF的长为( )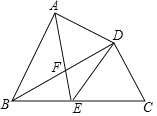
A.
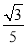 B.
B.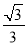 C.
C.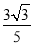 D.
D.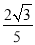
-
科目: 来源: 题型:
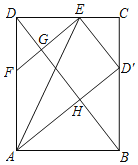
查看答案和解析>>【题目】如图,在矩形ABCD中,E为CD上一点,若△ADE沿直线AE翻折,使点D落在BC边上点D′处.F为AD上一点,且DF=CD',EF与BD相交于点G,AD′与BD相交于点H.D′E∥BD,HG=4,则BD=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=2x+4与x轴交于点A,与y轴交于点B,过点B的直线交x轴于点C,且△ABC面积为10.
(1)求点C的坐标及直线BC的解析式;
(2)如图1,设点F为线段AB中点,点G为y轴上一动点,连接FG,以FG为边向FG右侧作长形FGQP,且FG:GQ=1:2,在G点的运动过程中,当顶点Q落在直线BC上时,求点G的坐标;
(3)如图2,若M为线段BC上一点,且满足S△AMB=S△AOB,点E为直线AM上一动点,在x轴上是存在点D,使以点D,E,B,C为顶点的四边形为平行四边形?若存在,请直接写出点D的坐标;若不在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系内,
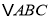 的三个顶点的分别为
的三个顶点的分别为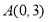 ,
,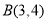 ,
,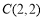 (正方形网格中每个小正方形的边长是一个单位长度).
(正方形网格中每个小正方形的边长是一个单位长度).
(1)在网格内画出
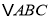 向下平移2个单位长度得到的
向下平移2个单位长度得到的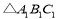 ,点
,点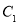 的坐标是________;
的坐标是________;(2)以点
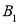 为位似中心,在网格内画出
为位似中心,在网格内画出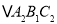 ,使
,使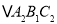 与
与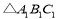 位似,且位似比为
位似,且位似比为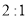 ,点
,点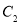 的坐标是________;
的坐标是________;(3)
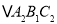 的面积是________平方单位.
的面积是________平方单位.
相关试题

