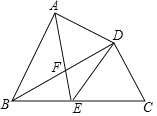
【题目】如图,在四边形ABCD中,对角线BD平分![]() ,
,![]() ,E为BC的中点,AE与BD相交于点F,若
,E为BC的中点,AE与BD相交于点F,若![]() ,则BF的长为( )
,则BF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】C
【解析】
连接DE,结合直角三角形性质得出CD=DE=1,BC=2,BD=![]() ,AB=
,AB=![]() ,然后利用角平分线性质证明出∠BDE=∠ABD,从而得出△AFB∽EFD,根据相似三角形对应边成比例进一步求解即可.
,然后利用角平分线性质证明出∠BDE=∠ABD,从而得出△AFB∽EFD,根据相似三角形对应边成比例进一步求解即可.
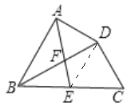
如图,连接DE,
∵![]() ,
,
∴△BDC是直角三角形,且∠C=60°,
∵E为BC的中点,
∴DE=BE=EC,
∴∠BDE=∠DBC=30°,
∴∠EDC=60°,
∴△DEC是等边三角形,
∴DE=EC=CD=1,
∴BC=2,
∴BD=![]() ,
,
∵BD平分![]() ,
,
∴∠ABD=∠DBC=30°,
∴AB=BD×cos30°=![]()
∵∠BDE=∠DBC=30°,
∴∠BDE=∠ABD,
∴△ABF∽△EDF,
∴![]() =
=![]() ,
,
∴BF=![]() ,
,
所以答案为C选项.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中,  是直线
是直线 上的一点,连接
上的一点,连接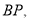 过点
过点 作
作 交直线
交直线 于点
于点 .
. 当点
当点 在线段
在线段 上时,如图①,求证:
上时,如图①,求证: ;
;
 当点
当点 在直线
在直线 上移动时,位置如图②、图③所示,线段
上移动时,位置如图②、图③所示,线段 与
与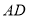 之间又有怎样的数量关系?请直接写出你的猜想,不需证明.
之间又有怎样的数量关系?请直接写出你的猜想,不需证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂以每千克200元的价格购进甲种原料360千克,用于生产A、B两种产品,生产1件A产品或1件B产品所需甲、乙两种原料的千克数如下表:
产品/原料
A
B
甲(千克)
9
4
乙(千克)
3
10
乙种原料的价格为每千克300元,A产品每件售价3000元,B产品每件售价4200元,现将甲种原料全部用完,设生产A产品x件,B产品m件,公司获得的总利润为y元.
(1)写出m与x的关系式;
(2)求y与x的关系式;
(3)若使用乙种原料不超过510千克,生产A种产品多少件时,公司获利最大?最大利润为多少?
-
科目: 来源: 题型:
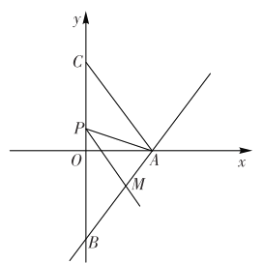
查看答案和解析>>【题目】如图,已知直线
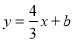 与
与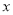 轴交于点
轴交于点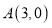 ,与
,与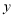 轴交于点
轴交于点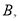 将
将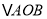 沿
沿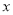 轴折叠,使点
轴折叠,使点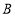 落在
落在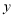 轴的点
轴的点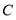 上,设
上,设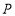 为线段
为线段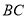 上的一个动点,点
上的一个动点,点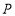 与点
与点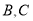 不重合,连接
不重合,连接 .以点
.以点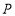 为端点作射线
为端点作射线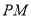 交线段
交线段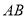 于点
于点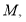 使
使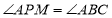 .
.
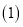 求点
求点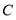 的坐标;
的坐标;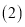 当
当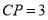 时,求直线
时,求直线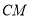 的解析式;
的解析式;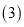 是否存在点
是否存在点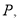 使
使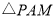 为直角三角形?若存在,请直接写出点
为直角三角形?若存在,请直接写出点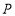 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E为CD上一点,若△ADE沿直线AE翻折,使点D落在BC边上点D′处.F为AD上一点,且DF=CD',EF与BD相交于点G,AD′与BD相交于点H.D′E∥BD,HG=4,则BD=__.
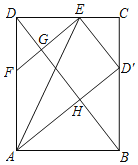
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=BC,点D、E分别在边BC,AC上,连接DE,且DE=DC.

(1)问题发现:若∠ACB=∠ECD=45°,则
 = .
= .(2)拓展探究:若∠ACB=∠ECD=30°,将△EDC饶点C按逆时针旋转α度(0°<α<180°),图2是旋转过程中的某一位置,在此过程中
 的大小有无变化?如果不变,请求出
的大小有无变化?如果不变,请求出 的值,如果变化,请说明理由;
的值,如果变化,请说明理由;(3)问题解决:若∠ABC=∠EDC=β(0°<β<90°),将△EDC旋转到如图3所示的位置时,则
 的值为 .(用含β的式子表示)
的值为 .(用含β的式子表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=2x+4与x轴交于点A,与y轴交于点B,过点B的直线交x轴于点C,且△ABC面积为10.
(1)求点C的坐标及直线BC的解析式;
(2)如图1,设点F为线段AB中点,点G为y轴上一动点,连接FG,以FG为边向FG右侧作长形FGQP,且FG:GQ=1:2,在G点的运动过程中,当顶点Q落在直线BC上时,求点G的坐标;
(3)如图2,若M为线段BC上一点,且满足S△AMB=S△AOB,点E为直线AM上一动点,在x轴上是存在点D,使以点D,E,B,C为顶点的四边形为平行四边形?若存在,请直接写出点D的坐标;若不在,请说明理由.

相关试题

