搜索
【题目】如图，在△ABC中，∠C=90°，点D是AB边上的一点，DE⊥AB于D，交AC于M，且ED=AC，过点E作EF∥BC分别交AB、AC于点F、N．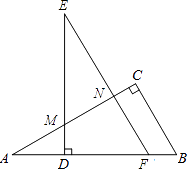 
（1）试说明：△ABC≌△EFD；
（2）若∠A=25°，求∠EMN的度数．
参考答案：
【答案】
（1）解：∵DE⊥AB于D，
∴∠EDF=90°，
∵∠C=90°，
∴∠C=∠EDF，
∵EF∥BC，
∴∠B=∠EFD，
在△ABC与△EFD中，
，
∴△ABC≌△EFD（AAS）
（2）解：∵∠EDF=90°，
∴∠ADM=180°﹣∠EDF=90°，
在△ADM中，∠A+∠AMD+∠ADM=180°且∠A=25°
∴∠AMD=180°﹣∠A﹣∠ADM=65°，
∴∠EMN=∠AMD=65°
【解析】（1）根据平行线的性质求得∠B=∠EFD，然后依据AAS即可证得△ABC≌△EFD；（2）根据三角形内角和定理求得∠AMD，然后根据对顶角相等即可求得．
【考点精析】掌握三角形的内角和外角是解答本题的根本，需要知道三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角．
-
科目： 来源： 题型：
查看答案和解析>>【题目】手机微信推出了抢红包游戏，它有多种玩法，其中一种为“拼手气红包”，用户设定好总金额以及红包个数后，可以生成不等金额的红包．现有一用户发了三个“拼手气红包”，总金额为3元，随机被甲、乙、丙三人抢到．
（1）判断下列事件中，哪些是确定事件，哪些是不确定事件？
①丙抢到金额为1元的红包；
②乙抢到金额为4元的红包
③甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多；
（2）记金额最多、居中、最少的红包分别为A，B，C．
①求出甲抢到红包A的概率；
②若甲没抢到红包A，则乙能抢到红包A的概率又是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】把下列的推理过程补充完整，并在括号里填上推理的依据：
如图，∠E=∠1，∠3+∠ABC=180°，BE是∠ABC的角平分线．
试说明：DF∥AB
解：因为BE是∠ABC的角平分线
所以（角平分线的定义）
又因为∠E=∠1（已知）
所以∠E=∠2（）
所以（）
所以∠A+∠ABC=180°（）
又因为∠3+∠ABC=180°（已知）
所以（同角的补角相等）
所以DF∥AB（）
-
科目： 来源： 题型：
查看答案和解析>>【题目】平面直角坐标系内，与点P（﹣3，2）关于原点对称的点的坐标是（ ）
A.（3，﹣2）
B.（2，3）
C.（2，﹣3）
D.（﹣3，﹣2） -
科目： 来源： 题型：
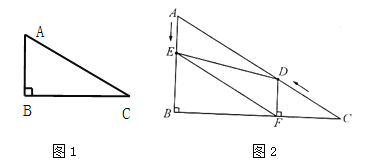
查看答案和解析>>【题目】如图1，在Rt△ABC中，∠B=90°，∠C=30°．
（1）求证：AB=
AC；并请你用文字叙述直角三角形的这条性质，把它写在下列横线上：；
（2）利用（1）题所得结论继续解答下列问题：
如图2，在Rt△ABC中，∠B=90°，BC=
，∠C=30°．点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F，连结DE、EF．①求证：四边形AEFD是平行四边形；
②当t为何值时，△DEF为直角三角形？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=x2﹣2x+m（m为常数）的图象与x轴的一个交点为（﹣1，0），则关于x的一元二次方程x2﹣2x+m=0的两个实数根是（ ）
A.x1=1，x2=2
B.x1=1，x2=3
C.x1=﹣1，x2=2
D.x1=﹣1，x2=3 -
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是( )
A. 所有的等腰三角形都是锐角三角形
B. 等边三角形属于等腰三角形
C. 不存在既是钝角三角形又是等腰三角形的三角形
D. 一个三角形里有两个锐角，则一定是锐角三角形
相关试题
