【题目】如图,DE⊥AB于E,DF⊥AC于F,AD平分∠BAC,BD=CD

(1)求证:BE=CF;
(2)已知AC=10,DE=4,BE=2,求△AEC的面积
参考答案:
【答案】(1)证明见解析;(2)36.
【解析】
(1)根据角平分线性质和全等三角形的性质得出即可;
(2)根据全等三角形的判定得出Rt△AED≌Rt△AFD,根据全等三角形的性质得出AE=AF,利用三角形面积公式即可得出答案.
(1)证明:∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,∠DEB=∠DFC=90°,
在Rt△BED和Rt△CFD中
![]() ,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFA=90°,
在Rt△AED和Rt△AFD中
![]() ,
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∵Rt△BED≌Rt△CFD,
∴CF=BE,
∵AC=10,BE=2,
∴AE=AF=10-2=8,DE=DF=4,
∴△AEC的面积=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B,F,C,E在同一直线上,AC,DF相交于点G,且△ABC≌△DEF
(1)若△ABC的周长为12cm,AB=3cm,BC=4cm,求DF的长.
(2)若DE⊥BC与点E,∠A=65°,求∠AGF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,D为CB上一点,过点D作DE⊥AB于点E.
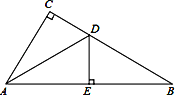
(1)若CD=DE,判断∠CAD与∠BAD的数量关系;
(2)若AE=EB,CB=10,AC=5,求△ACD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】鸡兔同笼问题是我国古代著名趣题之一,大约在 1500 年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡、兔同在一个笼子里,从上上面数,有 35 个头;从下面数,有 94 只脚 .求笼中各有几只鸡和兔?经计算可得( )

A. 鸡 20 只,兔 15 只 B. 鸡 12 只,兔 23 只
C. 鸡 15 只,兔 20 只 D. 鸡 23 只,兔 12 只
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了扶贫户学生好读书,读好书,某实验学校校友会在今年开学初,到新华书店采购文学名著和自然科学两类图书.经了解,购买30本文学名著和50本自然科学书共需2350元,20本文学名著比20本自然科学书贵500元.(注:所采购的文学名著价格都一样,所采购的自然科学书价格都一样)
(1)求每本文学名著和自然科学书的单价.
(2)若该校校友会要求购买自然科学书比文学名著多30本,自然科学书和文学名著的总数不低于80本,总费用不超过2400元,请求出所有符合条件的购书方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年4月4日,中国国际女足锦标赛半决赛在武汉进行,这场由中国队迎战俄罗斯队的比赛牵动着众多足球爱好者的心.在未开始检票入场前,已有1200名足球爱好者排队等待入场.假设检票开始后,每分钟赶来的足球爱好者人数是固定的,1个检票口每分钟可以进入40人.如果4个检票口同时检票,15分钟后排队现象消失;如果7个检票口同时检票,_____分钟后排队现象消失.
-
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用.
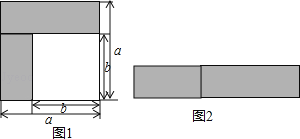
(1)如图1,阴影部分的面积是 (写成平方差的形式);
(2)如图2,若将阴影部分裁剪后重新拼成一个长方形,它的宽是 长是 ,面积可表示为 (写成多项式乘法的形式).
(3)运用以上得到的公式,计算:(x﹣2y+3z)(x+2y﹣3z)
相关试题

