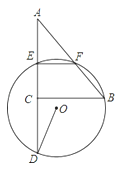
【题目】如图,△ABC中,AC=3,BC=4,∠ACB=90°,E、F分别为AC、AB的中点,过E、F两点作⊙O,延长AC交⊙O于D.若∠CDO=![]() ∠B,则⊙O的半径为( )
∠B,则⊙O的半径为( )
A. 4 B. 2![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
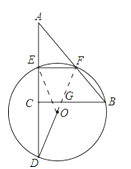
【解析】解:连接OF交BC于G,连接OE,∵E、F分别为AC、AB的中点,∴EF∥BC,EF=![]() BC=2,EC=
BC=2,EC=![]() AC=
AC=![]() .∵OE=OF,∴∠OEF=∠OFE.∵EF∥BC,∴∠DEF=∠DCB=90°,∴DF为直径,∴∠BGF=∠OFE.∵∠D=
.∵OE=OF,∴∠OEF=∠OFE.∵EF∥BC,∴∠DEF=∠DCB=90°,∴DF为直径,∴∠BGF=∠OFE.∵∠D=![]() ∠EOF,∠CDO=
∠EOF,∠CDO=![]() ∠B,∴∠EOF=∠B,∴∠OEF=∠BFG,∴∠BGF=∠BFG,∴BG=BF=
∠B,∴∠EOF=∠B,∴∠OEF=∠BFG,∴∠BGF=∠BFG,∴BG=BF=![]() ,CG=
,CG=![]() .∵EF∥BC,∴CD:DE=CG:EF,∴CD=3CE=
.∵EF∥BC,∴CD:DE=CG:EF,∴CD=3CE=![]() .在Rt△DFE中,EF=2,DE=6,DF=
.在Rt△DFE中,EF=2,DE=6,DF=![]() ,OD=
,OD=![]() .故选C.
.故选C.
-
科目: 来源: 题型:
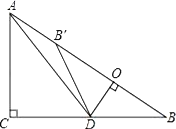
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两个直角顶点
 叠放在一起(如图①),其中
叠放在一起(如图①),其中 ,
,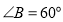 ,
, .
.
(1)若
 ,求
,求 的度数;
的度数;(2)试猜想
 与
与 的数量关系,请说明理由;
的数量关系,请说明理由;(3)若按住三角板
 不动,绕顶点
不动,绕顶点 转动三角板
转动三角板 ,试探究
,试探究 等于多少度时,
等于多少度时,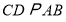 ,并简要说明理由.
,并简要说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:我们学习了整式的乘法,两个多项式相乘,我们可以运用法则,将其展开,例如:
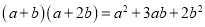 ,而将等号的左右两边互换,我们得到了
,而将等号的左右两边互换,我们得到了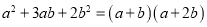 ,等号的左边是一个多项式,而右边是几个整式相乘的形式,我们规定将一个多项式写成几个整式相乘的形式,这种运算称之为“因式分解”
,等号的左边是一个多项式,而右边是几个整式相乘的形式,我们规定将一个多项式写成几个整式相乘的形式,这种运算称之为“因式分解”问题提出:
如何将
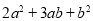 进行因式分解呢?
进行因式分解呢?问题探究:
数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性,从而可以帮助我们快速解题.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释
例如:我们可以通过表示几何图形面积的方法来快速的对多项式
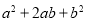 进行因式分解.
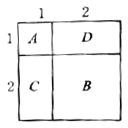
进行因式分解.如图所示边长为
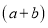 的大正方形是由1个边长为
的大正方形是由1个边长为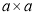 的正方形,2个边长为
的正方形,2个边长为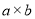 的长方形,1个边长为
的长方形,1个边长为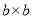 的正方形,
的正方形,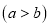 组成,我们可以用两种方法表示大正方形的面积,这个图形的面积可以表示成:
组成,我们可以用两种方法表示大正方形的面积,这个图形的面积可以表示成: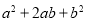 或
或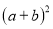
∴
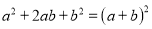
我们将等号左边的多项式写成了右边两个整式相乘的形式,从而成功的对多项式
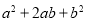 进行了因式分解
进行了因式分解请你类比上述方法,利用图形的几何意义对多项式
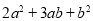 进行因式分解(要求自己构图并写出推证过程)
进行因式分解(要求自己构图并写出推证过程)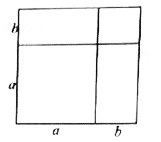
问题拓展:
如何利用图形几何意义的方法推导:
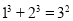 ?如图,
?如图,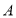 表示1个
表示1个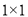 的正方形,即
的正方形,即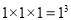 ,
,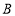 表示1个
表示1个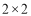 的正方形,
的正方形, 与
与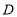 恰好可以拼成1个
恰好可以拼成1个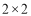 的正方形,因此:
的正方形,因此: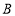 、
、 、
、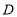 就可以表示2个
就可以表示2个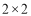 的正方形,即
的正方形,即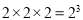 ,而
,而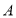 、
、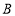 、
、 、
、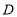 恰好可以拼成一个
恰好可以拼成一个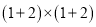 的大正方形.由此可得:
的大正方形.由此可得: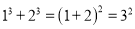
尝试解决:
请你类比上述推导过程,利用图形几何意义方法推导出
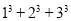 的值.
的值.(要求自己构造图形并写出推证过程).
解:
归纳猜想:
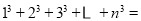 _________________.
_________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把菱形
 沿
沿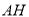 折叠,
折叠, 落在
落在 边上的
边上的 处,若
处,若 ,则
,则 的大小为( )
的大小为( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
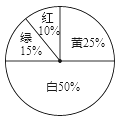
查看答案和解析>>【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘(如下图),并规定:购买100元的商品,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、绿、黄、白区域,那么顾客就可以分别得到80元、30元、10元、0元的购物券,凭购物券仍然可以在商场购物;如果顾客不愿意转转盘,那么可以直接获得购物券10元.
(1)每转动一次转盘所获购物券金额的平均数是多少?
(2)若在此商场购买100元的货物,那么你将选择哪种方式获得购物券?
(3)小明在家里也做了一个同样的转盘做实验,转10次后共获得购物券96元,他说还是不转转盘直接领取购物券合算,你同意小明的说法吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+3x+1﹣m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为负整数,求此时方程的根.
相关试题

