【题目】已知数轴上三点![]() 对应的数分别为-1,0,3,点
对应的数分别为-1,0,3,点![]() 为数轴上任意一点,其对应的数为
为数轴上任意一点,其对应的数为![]() .
.
(1)![]() 的长为_______;
的长为_______;
(2)如果点![]() 到点
到点![]() 、点
、点![]() 的距离相等,那么
的距离相等,那么![]() 的值是_______;
的值是_______;
(3)若点![]() 到点
到点![]() 、点
、点![]() 的距离之和是8,那么
的距离之和是8,那么![]() 的值是_______;
的值是_______;
(4)如果点![]() 以每分钟1个单位长度的速度从点
以每分钟1个单位长度的速度从点![]() 向左运动,同时点
向左运动,同时点![]() 和点
和点![]() 分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设
分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设![]() 分钟时点P到点
分钟时点P到点![]() 、点
、点![]() 的距离相等,那么
的距离相等,那么![]() 的值是_______.
的值是_______.
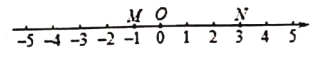
参考答案:
【答案】4 1 -3或5 4或![]()
【解析】
(1)![]() 的长即求MN的绝对值;
的长即求MN的绝对值;
(2)点![]() 到点
到点![]() 、点
、点![]() 的距离相等,P为MN的中点;
的距离相等,P为MN的中点;
(3)若点![]() 到点
到点![]() 、点
、点![]() 的距离之和是8,对P在M左边,P在MN之间和P在N右边进行分类讨论.
的距离之和是8,对P在M左边,P在MN之间和P在N右边进行分类讨论.
(4)分别根据①点M和点N在点P同侧时,②点M和点N在P异侧时进行解答.
(1)据图可得:![]()
(2)∵点![]() 到点
到点![]() 、点
、点![]() 的距离相等,即P为MN的中点.
的距离相等,即P为MN的中点.
P表示的![]()
(3)当P在M左边时,PM+PN=![]() ,解得
,解得![]() ;
;
当P在MN之间,PM+PN=MN=4≠8,舍去;
当P在N右边时,PM+PN=![]() ,解得
,解得![]() .
.
故![]() 或
或![]()
(4)设运动t分钟时,P到MN的距离相等.
由题意可以得![]() ,
,![]() ,
,![]()
①当点M和点N在点P同侧时,点M和点N重合,
∴![]() ,解得
,解得![]() ,符合题意.
,符合题意.
②当点M和点N在点P异侧时,点M位于点P左侧,点N位于点P的右侧(因为三个点都向左运动,出发时点M在点P左侧,且点M的运动速度大于点P的运动速度,所以点M永远位于点P的左侧)
∴![]() ;
;![]()
∴![]() 解得
解得![]() 符合题意.
符合题意.
∴综上所述![]() 的值是4或
的值是4或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在解决问题:已知a=
 ,求2a2﹣8a+1的值,他是这样分析与解的:
,求2a2﹣8a+1的值,他是这样分析与解的:∵a=
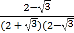 =
=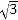 =2﹣
=2﹣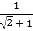
∴a﹣2=﹣
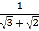
∴(a﹣2)2=3,a2﹣4a+4=3
∴a2﹣4a=﹣1
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1
请你根据小明的分析过程,解决如下问题:
(1)化简
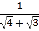 +
+ +
+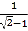 +…+
+…+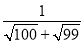
(2)若a=
 ,求4a2﹣8a+1的值.
,求4a2﹣8a+1的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的边AC为直径的⊙O恰为△ABC的外接圆,∠ABC的平分线交⊙O于点D,过点D作DE∥AC交BC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AB=25,BC=
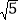 ,求DE的长.
,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),直线y=﹣
 x+
x+ 与边AB,BC分别相交于点M,N,函数y=
与边AB,BC分别相交于点M,N,函数y=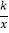 (x>0)的图象过点M.
(x>0)的图象过点M.(1)试说明点N也在函数y=
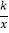 (x>0)的图象上;
(x>0)的图象上;(2)将直线MN沿y轴的负方向平移得到直线M′N′,当直线M′N′与函数y═
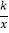 (x>0)的图象仅有一个交点时,求直线M'N′的解析式.
(x>0)的图象仅有一个交点时,求直线M'N′的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数
0
1
2
3
4
5
人数
11
15
23
28
18
5
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 ,该中位数的意义是 ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
-
科目: 来源: 题型:
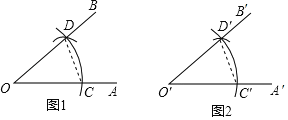
查看答案和解析>>【题目】已知:∠AOB.
求作:∠A'O'B',使∠A'O′B'=∠AOB
(1)如图1,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D;
(2)如图2,画一条射线O′A′,以点O′为圆心,OC长为半径间弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所而的弧交于点D′;
(4)过点D′画射线O′B',则∠A'O'B'=∠AOB.
根据以上作图步骤,请你证明∠A'O'B′=∠AOB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
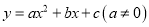 图象与x轴交于A,B两点,对称轴为直线x=2,下列结论:①abc>0; ②4a+b=0;③若点A坐标为(1,0),则线段AB=5; ④若点M(x1,y1)、N(x2,y2)在该函数图象上,且满足0<x1<1,2<x2<3,则y1<y2其中正确结论的序号为( )
图象与x轴交于A,B两点,对称轴为直线x=2,下列结论:①abc>0; ②4a+b=0;③若点A坐标为(1,0),则线段AB=5; ④若点M(x1,y1)、N(x2,y2)在该函数图象上,且满足0<x1<1,2<x2<3,则y1<y2其中正确结论的序号为( )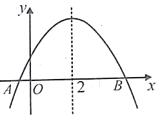
A. ①,② B. ②,③ C. ③,④ D. ②,④
相关试题

