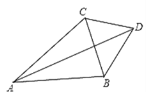
【题目】如图,在△ABC中,∠BAC=40°,∠ACB=60°,D为△ABC外一点,DA平分∠BAC,且CBD=50°,则∠DCB的度数是_______.
参考答案:
【答案】60°
【解析】
如图,延长AB到P,延长AC到Q,作DH⊥AP于H,DE⊥AQ于E,DF⊥BC于F.想办法证明DE=DF,推出DC平分∠QCB即可解决问题.
解:如图,延长AB到P,延长AC到Q,作DH⊥AP于H,DE⊥AQ于E,DF⊥BC于F.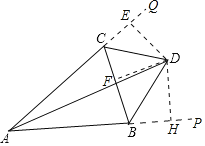
∵∠PBC=∠BAC+∠ACB=40°+60°=100°,∠CBD=50°,
∴∠DBC=∠DBH,
∵DF⊥BC,DH⊥BP,
∴DF=DH,
又∵DA平分∠PAQ,DH⊥PA,DE⊥AQ,
∴DE=DH,
∴DE=DF,
∴CD平分∠QCB,
∵∠QCB=180°-60°=120°,
∴∠DCB=60°,
故答案为60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:

(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=
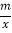 的图象的两个交点.
的图象的两个交点.(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)直接写出一次函数的值小于反比例函数值的x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某地上年度电价为0.8元,年用电量为1亿度,本年度计划将电价调至0.55﹣0.75之间,经测算,若电价调至x元,则本年度新增用电量y(亿度)与(x﹣0.4)(元)成反比例,又当x=0.65时,y=0.8.根据y与x之间的函数关系式,请你预算,如果每度电的成本价为0.3元,电价调至0.6元时,本年度电力部门的纯收入是_____亿元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2.
求证:(1)BE=DF;(2)AF∥CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】补全解答过程:
已知:如图,直线AB∥CD,直线EF与直线AB、CD分别交于点G、H,GM平分∠FGB,∠3=60°,求∠1的度数。

解:∵EF与CD交于点H(已知)
∴∠3=∠4(_______________)
∵∠3=60°(已知)
∴∠4=60°(______________)
∵AB∥CD,EF与AB、CD交于点G、H(已知)
∴∠4+∠FGB=180°(______________)
∴∠FGB=______°
∵GM平分∠FGB(已知)
∴∠1=_____°(______________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游商品经销店欲购进A、B两种纪念品,若用380元购进A种纪念品7件,B种纪念品8件;也可以用380元购进A种纪念品10件,B种纪念品6件.
(1)求A、B两种纪念品的进价分别为多少?
(2)若该商店每销售1件A种纪念品可获利5元,每销售1件B种纪念品可获利7元,该商店准备用不超过900元购进A、B两种纪念品40件,且这两种纪念品全部售出时总获利不低于216元,问应该怎样进货,才能使总获利最大,最大为多少?
相关试题

