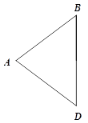
【题目】如图,在△ABD中,∠ABD = ∠ADB,分别以点B,D为圆心,AB长为半径在BD的右侧作弧,两弧交于点C,连接BC,DC和AC,AC与BD交于点O.
(1)用尺规补全图形,并证明四边形ABCD为菱形;
(2)如果AB = 5,![]() ,求BD的长.
,求BD的长.
参考答案:
【答案】(1)补全的图形如图所示.证明见解析;(2)BD=6.
【解析】
(1)根据作法画出对应的几何图形得到四边形ABCD;先利用∠ABD=∠ADB得到AB=AD.再利用作法得到BC=DC=AD=AB,从而可判断四边形ABCD为菱形;
(2)利用菱形的性质得到BD⊥AC,OB=OD,则根据![]() 计算出BO,从而得到BD的长.
计算出BO,从而得到BD的长.
(1)补全的图形如图所示.

证明:由题意可知BC = DC = AB,
∵ 在△ABD中,![]() ,
,
∴ AB = AD,
∴ BC = DC = AD = AB,
∴ 四边形ABCD为菱形;
(2)∵ 四边形ABCD为菱形,
∴ BD⊥AC,OB=OD,
在Rt△ABO中,![]() ,AB=5,
,AB=5,![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有红、黑两种颜色的球共60只,这些球除颜色外其余完全相同.为了估计红球和黑球的个数,七(2)班的数学学习小组做了摸球实验.他们将球搅匀后,从盒子里随机摸出一个球记下颜色,再把球放回盒子中,多次重复上述过程,得到表中的一组统计数据:
摸球的次数n
50
100
300
500
800
1000
摸到红球的次数m
14
33
95
155
241
298
摸到红球的频率

0.28
0.33
0.317
0.31
0.301
0.298
请估计:当次数n足够大时,摸到红球的频率将会接近_____.(精确到0.1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一组数据
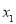 ,
,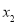 ,
,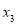 ,
,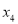 ,
,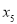 的方差是1,那么数
的方差是1,那么数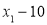 ,
,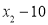 ,
,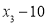 ,
,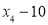 ,
,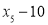 的方差是______.
的方差是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形
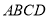 中,
中,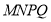 分别为边
分别为边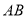 ,
,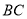 ,
,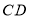 ,
,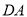 上的点(不与端点重合).对于任意菱形
上的点(不与端点重合).对于任意菱形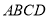 ,下面四个结论中:①存在无数个四边形
,下面四个结论中:①存在无数个四边形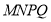 是平行四边形;②存在无数个四边形
是平行四边形;②存在无数个四边形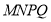 是菱形;③存在无数个四边形
是菱形;③存在无数个四边形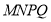 是矩形;④存在无数个四边形
是矩形;④存在无数个四边形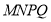 是正方形;所有正确结论的序号是______.
是正方形;所有正确结论的序号是______. -
科目: 来源: 题型:
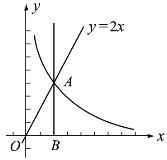
查看答案和解析>>【题目】如图,点
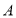 是直线
是直线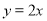 与反比例函数
与反比例函数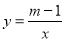 (
(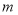 为常数)的图象的交点.过点
为常数)的图象的交点.过点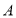 作
作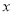 轴的垂线,垂足为
轴的垂线,垂足为 ,且
,且 .
.
(1)求点
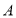 的坐标及
的坐标及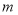 的值;
的值;(2)已知点
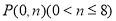 ,过点
,过点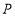 作平行于
作平行于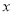 轴的直线,交直线
轴的直线,交直线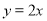 于点
于点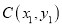 ,交反比例函数
,交反比例函数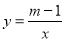 (
(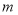 为常数)的图象于点
为常数)的图象于点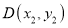 ,交垂线
,交垂线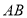 于点
于点 .若
.若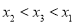 ,结合函数的图象,直接写出
,结合函数的图象,直接写出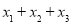 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:如图,
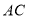 是
是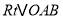 斜边上的高,到点
斜边上的高,到点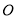 的距离等于
的距离等于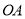 的所有点组成的图形记为
的所有点组成的图形记为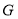 ,图形
,图形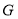 与
与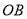 交于点
交于点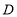 ,连接
,连接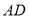 .
.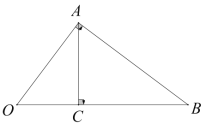
(1)依题意补全图形,并求证:
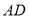 平分
平分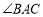 ;
;(2)如果
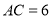 ,
,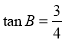 ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:在平面直角坐标系中,抛物线
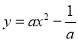 与
与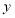 轴交于点
轴交于点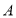 ,点
,点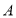 关于
关于 轴的对称点为点
轴的对称点为点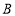 ,
,(1)求抛物线的对称轴;
(2)求点
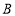 坐标(用含
坐标(用含 的式子表示);
的式子表示);(3)已知点
 ,
, ,若抛物线与线段
,若抛物线与线段 恰有一个公共点,结合函数图像,求
恰有一个公共点,结合函数图像,求 的取值范围.
的取值范围.
相关试题

