【题目】探索:小明和小亮在研究一个数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A,∠C的数量关系.
发现:在图1中,小明和小亮都发现:∠APC=∠A+∠C;
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A( )
∵PQ∥AB,AB∥CD.
∴PQ∥CD( )
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
小亮是这样证明的:过点作PQ∥AB∥CD.
∴∠APQ=∠A,∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
请在上面证明过程的过程的横线上,填写依据;两人的证明过程中,完全正确的是 .
应用:
在图2中,若∠A=120°,∠C=140°,则∠P的度数为 ;
在图3中,若∠A=30°,∠C=70°,则∠P的度数为 ;
拓展:
在图4中,探索∠P与∠A,∠C的数量关系,并说明理由.
参考答案:
【答案】两直线平行,内错角相等;平行于同一直线的两直线平行;小明的证法;100°;40°;
∠APC=∠A﹣∠C
【解析】
试题分析:过点P作AB的平行线,用相似的证明方法运用平行线的性质进行证明即可
试题解析:如图1,过点P作PQ∥AB, ∴∠APQ=∠A(两直线平行,内错角相等)
∵PQ∥AB,AB∥CD. ∴PQ∥CD(平行于同一直线的两直线平行) ∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C 即∠APC=∠A+∠C,
故两人的证明过程中,完全正确的是小明的证法;
如图2,过点P作PE∥AB, ∴∠APE+∠A=180°,∠A=120°,∴∠APE=60°,
∵PE∥AB,AB∥CD. ∴PE∥CD(平行于同一直线的两直线平行)
∴∠CPE+∠C=180°,∠C=140°,∴∠CPE=40°, ∴∠APC=∠APE+∠CPE=100°;
如图3,过点P作PF∥AB, ∴∠APF=∠A, ∵PF∥AB,AB∥CD. ∴PF∥CD,
∴∠CPF=∠C ∴∠CPF﹣∠APF=∠C﹣∠A 即∠APC=∠C﹣∠A=40°;
如图4,过点P作PG∥AB, ∴∠APG+∠A=180°,∴∠APG=180°﹣∠A
∵PG∥AB,AB∥CD, ∴PG∥CD,(平行于同一直线的两直线平行)
∴∠CPG+∠C=180°,∴∠CPG=180°﹣∠C ∴∠APC=∠CPG﹣∠APG=∠A﹣∠C.




-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 为
为 上的一点,按下列要求进行作图.
上的一点,按下列要求进行作图.(1)作
 的平分线
的平分线 .
.(2)在
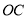 上取一点
上取一点 ,使得
,使得 .
.(3)爱动脑筋的小刚经过仔细观察后,进行如下操作:在边
 上取一点
上取一点 ,使得
,使得 ,这时他发现
,这时他发现 与
与 之间存在一定的数量关系,请写出
之间存在一定的数量关系,请写出 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
原题:如图①,点
 分别在正方形
分别在正方形 的边
的边 上,
上,  ,连接
,连接 ,则
,则 ,试说明理由.
,试说明理由.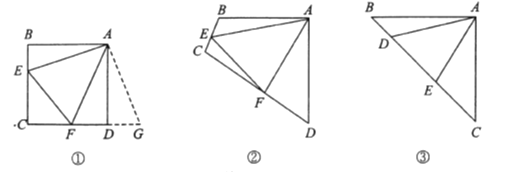
(1)思路梳理
因为
 ,所以把
,所以把 绕点
绕点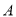 逆时针旋转90°至
逆时针旋转90°至 ,可使
,可使 与
与 重合.因为
重合.因为 ,所以
,所以 ,点
,点 共线.
共线.根据 ,易证
 ,得
,得 .请证明.
.请证明.(2)类比引申
如图②,四边形
 中,
中,  ,
,  ,点
,点 分别在边
分别在边 上,
上,  .若
.若 都不是直角,则当
都不是直角,则当 与
与 满足等量关系时,
满足等量关系时,  仍然成立,请证明.
仍然成立,请证明.(3)联想拓展
如图③,在
 中,
中,  ,点
,点 均在边
均在边 上,且
上,且 .猜想
.猜想 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x2-4x+2=0; (2)x2+3x+2=0;
(3)3x2-7x+4=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6
 ,那么AC=_____.
,那么AC=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】李明准备进行如下操作试验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
相关试题

