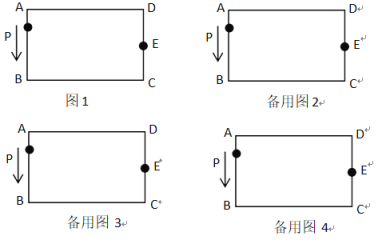
【题目】如图,长方形ABCD,AB=CD=4,BC=AD=8,∠A=∠B=∠C=∠D=90°,E为CD边的中点,P为长方形ABCD边上的动点,动点P从A出发,沿着A B C E运动到E点停止,设点P经过的路程为![]() ,APE的面积为
,APE的面积为![]() .
.
(1)当![]() 时,在图1中画出草图,并求出对应
时,在图1中画出草图,并求出对应![]() 的值;
的值;
(2)利用备用图画出草图,写出![]() 与
与![]() 之间的关系式.
之间的关系式.
参考答案:
【答案】(1)15;(2)①当0≤x≤4时,y=4x;②当4<x≤12时,y=20-x;③当12<x≤14时,y=56-4x
【解析】
(1)先根据题意画出草图,再利用三角形面积求法S△APE=S长方形ABCD-S△APB-S△PCE-S△ADE得出答案即可;
(2)分3种情况来解答,利用当0≤x≤4时,当4<x≤12时,当12<x≤14时,分别求出y与x的函数关系式即可.
(1)当![]() 时,点P在BC边上,如图1,
时,点P在BC边上,如图1,
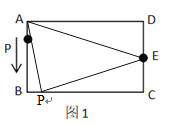
∵长方形ABCD,AB=CD=4,BC=AD=8,∠A=∠B=∠C=∠D=90°,E为CD边的中点,
∵x=5
∴BP=x-4=1,CP=12-x=7,CE=ED=2
∴S△APE=S长方形ABCD-S△APB-S△PCE-S△ADE
=8×4-![]() ×4×1-
×4×1-![]() ×7×2-
×7×2-![]() ×2×8
×2×8
=32-2-7-8
=15
∴y=15
(2)分3种情况来讨论,
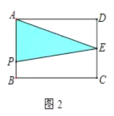
①当0≤x≤4时,如图2,AP=x,
S△APE=![]() ·AP·BC=
·AP·BC=![]() ·x·8=4x
·x·8=4x
∴y=4x
②当4<x≤12时,如图3,BP=x-4,PC=12-x,
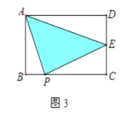
S△APE=S长方形ABCD-S△APB-S△PCE-S△ADE
=4×8-![]() ×(x-4) ×4-
×(x-4) ×4-![]() ×2×(12-x)-
×2×(12-x)- ![]() ×2×8
×2×8
=32-2x+8-12+x-8
=20-x
∴y=20-x
③当12<x≤14时,如图4,
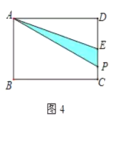
PE=4+8+2-x=14-x
S△AEP=![]() ·PE·8=
·PE·8=![]() ×8×(14-x)=56-4x
×8×(14-x)=56-4x
∴y=56-4x
综上所述:①当0≤x≤4时,y=4x;②当4<x≤12时,y=20-x;③当12<x≤14时,y=56-4x
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F.

(1)请连结AF、BD,试判断四边形ABDF是何种特殊四边形,并说明理由.
(2)若AB=4,BC=5,CD=6,求△BCF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E.F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
求证:(1)四边形AECF是平行四边形。(2)EF与GH互相平分。

-
科目: 来源: 题型:
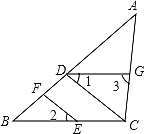
查看答案和解析>>【题目】如图,点D、F在线段AB上,点E、G分别在线段BC和AC上,CD∥EF,∠1=∠2.
(1)判断DG与BC的位置关系,并说明理由;
(2)若DG是∠ADC的平分线,∠3=85°,且∠DCE:∠DCG=9:10,AB与CD有怎样的位置关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
若一个三位数是
 ,则百位上数字为
,则百位上数字为 ,十位上数字为
,十位上数字为 ,个位上数字为
,个位上数字为 ,这个三位数可表示为
,这个三位数可表示为 ;现有一个正的四位数
;现有一个正的四位数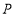 ,千位上数字为
,千位上数字为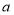 ,百位上数字为
,百位上数字为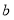 ,十位上数字为
,十位上数字为 ,个位上数字为
,个位上数字为 ,若交换千位与个位上的数字也交换百位与十位上的数字,则可构成另一个新四位数
,若交换千位与个位上的数字也交换百位与十位上的数字,则可构成另一个新四位数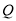 .
.(1)四位数
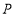 可表示为:
可表示为:  (用含
(用含 的代数式表示);
的代数式表示);(2)若
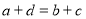 ,试说明:
,试说明: 能被
能被 整除.
整除. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,菱形ABCD中,过AD的中点E作AC的垂线EF,交AB于点M,交CB的延长线于点F.如果FB的长是
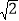 ,∠AEM=30°.求菱形ABCD的周长和面积.
,∠AEM=30°.求菱形ABCD的周长和面积.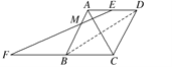
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AC、BD相交于O,AE平分∠BAD,交BC于E,若∠CAE=15°,求∠BOE的度数.

相关试题

