【题目】下面是数学课堂的一个学习片段, 阅读后, 请回答下面的问题:
学习勾股定理有关内容后, 张老师请同学们交流讨论这样一个问题: “已知直角三角形ABC的两边长分别为3和4, 请你求出第三边.”
同学们经片刻的思考与交流后, 李明同学举手说: “第三边长是5”; 王华同学说: “第三边长是![]() .” 还有一些同学也提出了不同的看法……
.” 还有一些同学也提出了不同的看法……
(1)假如你也在课堂上, 你的意见如何? 为什么?
(2)通过上面数学问题的讨论, 你有什么感受? (用一句话表示)
参考答案:
【答案】(1)5或![]() (2)见解析
(2)见解析
【解析】本题考查了勾股定理的运用
(1)应分情况考虑:当4为直角边长时,第三边长为5;当4为斜边长时,第三边长为![]() ;
;
(2)在已知条件中没有明确斜边的时候,一定要注意分情况讨论计算,注意思维的严密性.
(1)分两种情况:当4为直角边长时,第三边长为5;当4为斜边长时,第三边长为![]() ;
;
(2)考虑问题要严密,没有明确直角边和斜边的时候,注意分情况计算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A.
 B.
B.  C.
C. 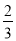 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c.
(1)若a∶b=3∶4,c=75cm,求a、b;
(2)若a∶c=15∶17,b=24,求△ABC的面积;
(3)若c-a=4,b=16,求a、c;
(4)若∠A=30°,c=24,求c边上的高hc;
(5)若a、b、c为连续整数,求a+b+c.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分7分)在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A处。另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,求这棵树高。

-
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)下面是小马虎解的一道题
题目:在同一平面上,若∠BOA=70°,∠BOC=15°求∠AOC的度数.
解:根据题意可画出图,

∵∠AOC=∠BOA-∠BOC
=70°-15°
=55°,
∴∠AOC=55°.
若你是老师,会判小马虎满分吗?若会,说明理由.若不会,请将小马虎的的错误指出,并给出你认为正确的解法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)用适当的方法解方程:
①(x﹣2)2=2x﹣4
②x2﹣2x﹣8=0.
(2)先化简,再求值: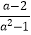 ÷(
÷( 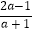 ﹣a+1),其中a是方程x2﹣x=6的根.
﹣a+1),其中a是方程x2﹣x=6的根.
相关试题

