【题目】为响应国家的“节能减排”政策,某厂家开发了一种新型的电动车,如图,它的大灯A射出的光线AB、AC与地面MN的夹角分别为22°和31°,AT⊥MN,垂足为T,大灯照亮地面的宽度BC的长为![]() m.
m.

(1)求BT的长(不考虑其他因素).
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到电动车完全停下所行驶的距离叫做最小安全距离.某人以20km/h的速度驾驶该车,从做出刹车动作到电动车停止的刹车距离是![]() ,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
(参考数据:sin22°≈![]() ,tan22°≈
,tan22°≈![]() ,sin31°≈
,sin31°≈![]() ,tan31°≈
,tan31°≈![]() )
)
参考答案:
【答案】(1)![]() ;(2)该车大灯的设计不能满足最小安全距离的要求.
;(2)该车大灯的设计不能满足最小安全距离的要求.
【解析】试题分析:(1)在直角△ACT中,根据三角函数的定义,若AT=3x,则CT=5x,在直角△ABT中利用三角函数即可列方程求解;
(2)求出正常人作出反应过程中电动车行驶的路程,加上刹车距离,然后与BT的长进行比较即可.
解:(1)根据题意及图知:∠ACT=31°,∠ABT=22°
∵AT⊥MN
∴∠ATC=90°
在Rt△ACT中,∠ACT=31°
∴tan31°=![]()
可设AT=3x,则CT=5x
在Rt△ABT中,∠ABT=22°
∴tan22°=![]()
即: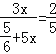
解得:![]()
∴![]() ,
,
∴![]() ;
;
(2)![]() ,
,
![]() ,
,
![]()
∴该车大灯的设计不能满足最小安全距离的要求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据报道,22年前,中国开始接入国际互联网,至今已有4 130 000家网站,将数4 130 000用科学记数法表示为( )
A. 413×104 B. 41.3×105 C. 4.13×106 D. 0.413×107
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的有( )
①Rt△ABC中,已知两边长分别为3和4,则第三边长为5;
②有一个内角等于其他两个内角和的三角形是直角三角形;
③三角形的三边分别为a,b,C,若a2+c2=b2,那么∠C=90°;
④若△ABC中,∠A:∠B:∠C=1:5:6,则△ABC是直角三角形.
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中,AB=10cm,BC=8cm,点E是CD的中点,动点P从A点出发,以每秒2cm的速度沿A→B→C→E运动,最终到达点E.若点P运动的时间为x秒,那么当x= 时,△APE的面积等于32.
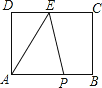
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为4,B是⊙O外一点,连接BO,且BO=6,延长BO交⊙O于点A,D是⊙O上一点,过点A作直线BD的垂线AC,垂足为C,连接AD,且AD平分∠BAC .
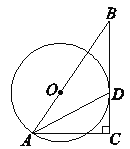
(1)求证:BD是⊙O的切线 ;
(2)求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两圆半径分别为3、5,圆心距为8,则这两圆的位置关系为( )
A.外离
B.内含
C.相交
D.外切 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形的三边长为1.5,2,2.5,那么这个三角形最短边上的高为______.
相关试题

