【题目】如图,已知数轴上点![]() 对应的数为6,
对应的数为6,![]() 是数轴上
是数轴上![]() 点左边的一点,
点左边的一点,![]() =10,动点
=10,动点![]() 从
从![]() 点出发,沿着数轴正方向向右匀速运动,若
点出发,沿着数轴正方向向右匀速运动,若![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,点
的中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若有变化,说明理由;若没有变化,请求出
的长度是否发生变化?若有变化,说明理由;若没有变化,请求出![]() 的长度.
的长度.
![]()
参考答案:
【答案】不变;MN长度恒等于5
【解析】
分类讨论:①当点P在点A、B两点之间运动时,②当点P运动到点B的左侧时,利用中点的定义和线段的和差易求出MN.
线段MN的长度不发生变化,等于5.
理由如下:
分两种情况:
①当点P在点A、B两点之间运动时:
![]()
MN=MP+NP=![]() AP+
AP+![]() BP=
BP=![]() (AP+BP)=
(AP+BP)=![]() AB=5;
AB=5;
②当点P运动到点B的左侧时:
![]()
MN=MP-NP=![]() AP-
AP-![]() BP=
BP=![]() (AP-BP)=
(AP-BP)=![]() AB=5,
AB=5,
∴综上所述,线段MN的长度不发生变化,其值为5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解嘉峪关初三学生体育测试自选项目的情况,从我市初三学生中随机抽取中部分学生的自选项目进行统计,绘制了扇形统计图和频数分布直方图,请根据图中信息,回答下列问题:
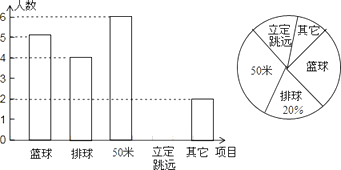
(1)本次调查共抽取了名学生;
(2)此次调查报其他项目的人数占了(填百分数),报立定跳远的人数是;
(3)扇形统计图中50米部分所对应的圆心角的度数是;
(4)我市共有初三学生3000名,估计我市有多少名学生选报篮球项目? -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校开展课外体育活动,决定开设
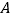 :篮球、
:篮球、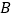 :乒乓球、
:乒乓球、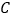 :踢毽子、
:踢毽子、 :跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.
:跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.(1)求出“最喜欢篮球”部分的扇形的圆心角度数;
(2)请把条形统计图补充完整;
(3)若该校有学生1000人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数
 (k≠0)在第一象限内的图像经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图像经过点D、E,且tan∠BOA=  .
.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图像与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若样本x1+1,x2+1,…,xn+1的平均数为10,方差为2,则对于样本x1+2,x2+2,…,xn+2,下列结论正确的是( )
A. 平均数为10,方差为2 B. 平均数为11,方差为3
C. 平均数为11,方差为2 D. 平均数为12,方差为4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.
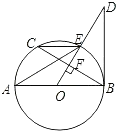
(1)判断直线BD和⊙O的位置关系,并给出证明;
(2)当AB=10,BC=8时,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】班主任要从甲、乙两名跳远运动员中挑选一人参加校运动会比赛.在最近的10次选拔赛中,他们的成绩如下(单位:cm):
甲
585
596
610
598
612
597
604
600
613
601
乙
613
618
580
574
618
593
585
590
598
624
(1)他们的平均成绩分别是多少?
(2)甲、乙两名运动员这10次比赛成绩的极差、方差分别是多少?
(3)怎样评价这两名运动员的运动成绩?
(4)历届比赛表明,成绩达到5.96m就有可能夺冠,你认为为了夺冠应选择谁参加这项比赛?如果历届比赛成绩表明,成绩达到6.10m就能打破记录,那么你认为为了打破记录应选择谁参加这项比赛?
相关试题

