【题目】若样本x1+1,x2+1,…,xn+1的平均数为10,方差为2,则对于样本x1+2,x2+2,…,xn+2,下列结论正确的是( )
A. 平均数为10,方差为2 B. 平均数为11,方差为3
C. 平均数为11,方差为2 D. 平均数为12,方差为4
参考答案:
【答案】C
【解析】解:由题知,x1+1+x2+1+x3+1+…+xn+1=10n,∴x1+x2+…+xn=10n﹣n=9n
S12=![]() [(x1+1﹣10)2+(x2+1﹣10)2+…+(xn+1﹣10)2]=
[(x1+1﹣10)2+(x2+1﹣10)2+…+(xn+1﹣10)2]= ![]() [(x12+x22+x32+…+xn2)﹣18(x1+x2+x3+…+xn)+81n]=2,∴(x12+x22+x32+…+xn2)=83n
[(x12+x22+x32+…+xn2)﹣18(x1+x2+x3+…+xn)+81n]=2,∴(x12+x22+x32+…+xn2)=83n
另一组数据的平均数=![]() [x1+2+x2+2+…+xn+2]=
[x1+2+x2+2+…+xn+2]= ![]() [(x1+x2+x3+…+xn)+2n]=
[(x1+x2+x3+…+xn)+2n]= ![]() [9n+2n]=
[9n+2n]= ![]() ×11n=11,另一组数据的方差=
×11n=11,另一组数据的方差=![]() [(x1+2﹣11)2+(x2+2﹣11)2+…+(xn+2﹣11)2]
[(x1+2﹣11)2+(x2+2﹣11)2+…+(xn+2﹣11)2]
=![]() [(x12+x22+…+xn2)﹣18(x1+x2+…+xn)+81n]=
[(x12+x22+…+xn2)﹣18(x1+x2+…+xn)+81n]= ![]() [83n﹣18×9n+81n]=2.故选C.
[83n﹣18×9n+81n]=2.故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品店购进一批单件为40元的球服,如果按单价60元销售样,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套.设销售单价为x(x≥60)元,销售量为y套.
(1)求出y与x的函数关系式;
(2)当销售单件为多少元时,月销售额为14000元?
(3)当销售单价为多少元时,才能在一个月内获得最大利润?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】在学校开展的小制作评比活动中,二年级六个班都参加了比赛,根据他们上交作品的件数,绘制直方图如右.已知从左至右各长方形高的比为2∶3∶4∶2∶3∶1,小制作件数最多的三班上交了16件.经评选各班获奖件数如下表:

在这次评选中,获奖率最高的两个班级依次是( ).
A. 5班、3班 B. 3班、4班 C. 5班、6班 D. 6班、5班
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB与CD交于点O,OM为射线.
(1)写出∠BOD的对顶角;
(2)写出∠BOD与∠COM的邻补角;
(3)已知∠AOC=70°,∠BOM=80°,求∠DOM和∠AOM的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在线段上依次添加1个点,2个点,3个点,……,原线段上所成线段的总条数如下表:
添加点数
1
2
3
4
线段总条数
3
6
10
15
若在原线段上添加n个点,则原线段上所有线段总条数为( )
A. n+2 B. 1+2+3+…+n+n+1 C. n+1 D.
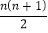
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是某俱乐部篮球队队员年龄结构直方图,根据图中信息解答下列
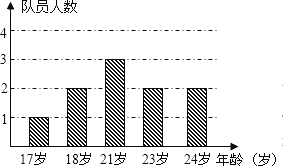
问题:
(1)该队队员年龄的平均数;
(2)该队队员年龄的众数和中位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线与x交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3).
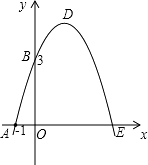
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积.
相关试题

